Gegeben sind die Funktionsscharen
fa(x) = -(1/18)*x3 + (1/2)*a*x2
g
a(x) = (a/6)*x^2
a∈ R, a>0
Die Graphen der Kurvenscharen werden mit Fa bzw. Ga bezeichnet.
Der Graph von F
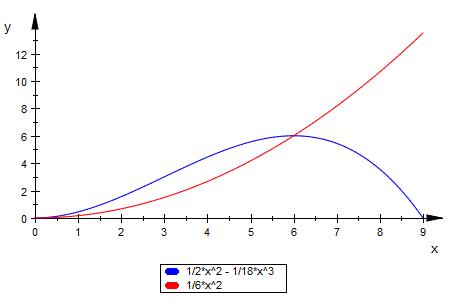
1 schließt im ersten Quadranten mit der x – Achse
eine Fläche ein. Der Graph von G
1 zerlegt diese Fläche in zwei Teilflächen.
Zeigen Sie, dass das Verhältnis der Teilflächen von a unabhängig ist.
Nullstellen f
f ( x ) = -1/18 * x^3 + 1/2 * a * x2
f ( x ) = x^2 * ( -1/18 * x + 1/2 * a )
x^2 * ( -1/18 * x + 1/2 * a ) = 0
x^2 = 0 => x = 0
und
-1/18 * x + 1/2 * a = 0
1 /18 x = 1/2 * a
x = 9 a
Schnittstelle f und g
f ( x ) = g ( x )
-1/18 * x^3 + 1/2 * a * x2 = (a/6)*x^2
x^2 * ( -1/18 * x + 1/2 * a ) = (a/6)*x^2
x = 0
-1/18 * x + 1/2 * a = a / 6
-1 /1 8 * x = a / 6 - 1/2 * a
1 / 18 * x = 1 / 3 * a
x = 6 * a
Flächen
F1 : ∫ g ( x ) zwischen 0 und 6 * a
F2 : ∫ f ( x ) zwischen 0 und 6 * a
F3 : ∫ f ( x ) zwischen 6 * a und 9 * a
F2 - F1
zu
F1 + F3
Bin gern weiter behilflich.
mfg