Aufgabe:
Zur Bestimmung der Höhe h einer Kletterwand werden mithilfe eines Messgeräts 2 Winkel gemessen. Das Messgerät steht 1,60 m über dem waagerechten Erdboden.
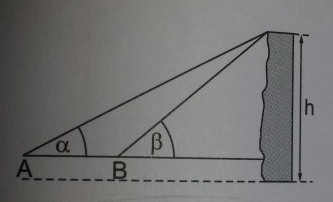
Bestimmen Sie die Höhe der Kletterwand.
Strecke AB=10m; Winkel alpha =42,4°;beta=65,6°
Ansatz/Problem:
Stimmt mein Rechenweg?
tan 65.6°=h/x
tan 42,4°=h/(x+10 m)
tan 65.6°x=tan 42,4°*(x+10m)
tan 65.6°x=tan 42,4°x + 9,13 m I-tan 42,4°x
1,29x =9,13 m I:1,29x
x =7,08m
tan 65,6°= h/7,08m
h =tan 65,6°* 7,08m
h =15,61m
15,61 m + 1,60 m=17,21 m
Die Kletterwand hat eine Höhe von 17,21m.