Zeigen Sie, dass die Funktionsvorschrift die Silhouette des Tiegels beschreibt. Rotationskörper skizzieren.

Question

Aufgabe:

Es soll das exakte Volumen eines Porzellantiegels berechnet werden.

1.1. Zeigen Sie, dass die Funktionsvorschrift \( f(x)=\frac{20}{21} x^{2}-\frac{20}{21} \) die Silhouette des stehenden Tiegels beschreibt.

1.2. Skizzieren Sie den Rotationskörper in einem geeigneten Koordinatensystem.

1.3. Berechnen Sie das Volumen mittels Integralrechnung.

1.4. Berechnen Sie die genaue Füllhöhe des Tiegels, wenn dieser mit einem Volumen von \( V=25 \mathrm{~cm}^{3} \) gefüllt ist.

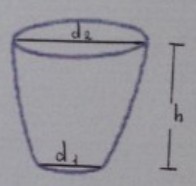
\( d_{1}=2 \mathrm{~cm} \)
\( d_{2}=5 \mathrm{~cm} \)
\( h=5 \mathrm{~cm} \)

Ansatz/Problem:

Ich weiß, dass ich die Umkehrfunktion bilden muss, aber erst mal muss ich ja bei 1.1 die Funktion bestätigen, aber wie?

Answer 1

Silhoutte

~plot~ 20 / 21 * x^2 - 20 / 21~plot~ 

Comments

Hier meine Berechnungen

Fehlerhinweis
Es muß heißen
V ( x ) = π* [ 21 / 40 * x^2 + x ]₀⁵
V = 56.94

---

Hier die Skizze der Umkehrfunktion
( Rotationskörper )

---

V ( x ) = π* [ 21 / 40 * x² + x ]₀^x = 25
π* ( 21 / 40 * x² + x ) = 25

Zum Selberausrechnen.
Ergebnis x = 3.06

---

Hi Georg, ich habe aus Interesse deine Rechnung oben nach TeX übertragen und dabei auf die Zeit geschaut. Es hat mich 5 min gekostet (ich bin aber noch lange kein Pro):

$$ f(x) = y = \frac{20}{21}x^2-\frac{20}{21} \\ x = \frac{20}{21}y^2 - \frac{20}{21} \\ x = \frac{20}{21} · (y^2-1) \\ y^2 - 1 = \frac{21x}{20} \\ y^2 = \frac{21x}{20} + 1 \\ A(x) = y^2 · \pi \\ A(x) = (\frac{21x}{20} + 1)^2 · \pi \\ \text {Stammfunktion} \\ \pi · \int_{}^{}\frac{21}{20}·x+1 \ dx \\ \pi · (\frac{21·x^2}{20·2}+x) \\ V(x) = \pi · [ \frac{21}{40} · x^2 + x ]_{0}^{5} \\ V(x) = 56,94 $$

Zusätzlich die Graphen mit 2 bis 3 min:

~plot~ ((21/20*x+1)^{1/2})*(x>0);(-(21/20*x+1)^{1/2})*(x>0) ~plot~

Und falls beim Übertragen ein Fehler entsteht, können wir schnell editieren :)

Schöne Grüße
Kai

Answer 2

Volumen V =  1/3 π *  h  ( r1²  +r2² + r1 * r2 )   ----->  51 cm³ !

Hast du das auch ?

Comments

ich habe V=

 52,20 cm3

---

Damit wir die Volumenberechnung einmal klären

V ( x ) = π* [ 21 / 40 * x² + x ]₀^x
V ( x ) = π* ( 21 / 40 * x² + x )
V ( 5 ) = π* ( 21 / 40 * 5² + 5 )
V = 56.94

Zur Herleitung der Volumenformel bitte in meiner
Antwort nachsehen.

mfg Georg