Modelliere jene Regressionsgerade, die den Trend von 2008 bis 2012

Question

Hallo

Statistik

Jahr	Beförderte Personen in der Luft in Mio
2008	24,8
2009	22,7
2010	24,5
2011	25,8
2012	26,6

a) Modelliere jene Regressionsgerade, die den Trend von 2008 bis 2012 für die beförderten Personen " in der Luft" beschreibt.

ich habe : y=0,67x-1321,8

b) Interpretiere mithilfe des Korrealationskoeffizient die Aussagekraft der Trendlinie. 

ich habe: R²=0,5155  r= 2Wurzel aus 0,5155²= 0,7179...

wie kann ich das Intepretieren und ich glaube meine Ergbenisse sind falsch ??

c) Gib eine Prognose für die Jahre 2014 und 2015 wie funktioniert das ? wie kann ich das rechnen ?

Danke für Ihre Antworten

Answer 1

Du liegst mit allem richtig. Für die Prognose musst du nur die entsprechenden x-Werte einsetzen. Also einfach 2014 bzw. 2015 einsetzen und gucken, was du für \(\hat{y}\) kriegst. Um die Ergebnisse zu interpretieren, solltest du dir zunächst noch mal die Definitionen anschauen. Vielleicht kommst du dann schon von selbst drauf? Ansonsten noch mal nachfragen :)

Das spuckt R aus:

##

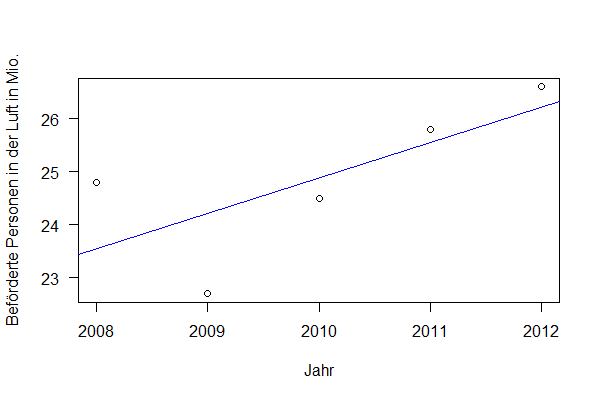
## Call:

## lm(formula = y ~ x)

##

## Residuals:

## 1 2 3 4 5

## 1.26 -1.51 -0.38 0.25 0.38

##

## Coefficients:

## Estimate Std. Error t value Pr(>|t|)

## (Intercept) -1321.820 753.773 -1.754 0.178

## x 0.670 0.375 1.787 0.172

##

## Residual standard error: 1.186 on 3 degrees of freedom

## Multiple R-squared: 0.5155, Adjusted R-squared: 0.354

## F-statistic: 3.192 on 1 and 3 DF, p-value: 0.172