Aufgabe:
Ein Rechteck mit U => max, soll in einen Halbkreis eingeschoben werden.
(Wenn U => max im Halbkreis gilt, muss es doch auch in einem Halbkreis gelten, siehe Skizze.)
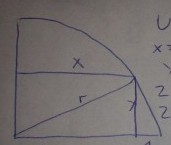
Ansatz/Problem:
Wie lässt sich diese Aufgabe lösen? Vom Prinzip her dürfte ich doch nicht falsch liegen?
\( y=2 x+2 y \)
\( x=\sqrt{r^{2}-y^{2}} \)
\( y=\sqrt{r^{2}-x^{2}} \)
\( 2 x+2 \sqrt{r^{2}-x^{2}} \)
\( 2 x+\sqrt{4 r^{2}-4 x^{2}} \)
\( U^{\prime}=2+\frac{1}{2 \sqrt{4 r^{2}-4 x^{2}}} \cdot(-8 x) \)
\( \begin{aligned} 4 r^{2}-4 x^{2} &=4 x^{2} \\ 4 r^{2} &=8 x^{2} \\ x &=\sqrt{\frac{1}{2}} \cdot r \end{aligned} \)