Aufgabe:
Eine Leitung soll zu einem Haus verlegt werden. Verläuft sie entlang der Straße (die 50 km Linie) kostet ein Laufmeter 165 €, im Gelände nur 120 €.
Wo muss die Abzweigung gewählt werden bzw. wie groß muss x sein, damit die Gesamtkosten minimal sind?
(Die Kilometer wurden bei mir zu Meter, da es aufs Ergebnis keine Auswirkungen hat.)
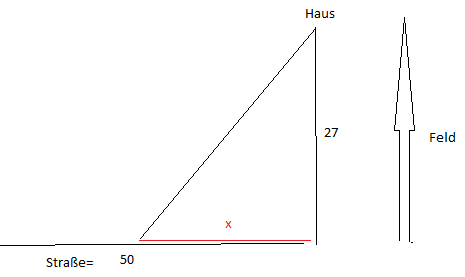
Laut Lösung sollte x ≈ 36 km sein.
Ansatz/Problem:
Egal wie oft ich es durchrechne... Ich komme einfach nicht aus richtige Ergebnis, da ich immer um ca 3 daneben liege. (Es kann kein Rundungsfehler sein - Die Zahlen wurden im Taschenrechner gespeichert.)