Einem Kreis soll ein Rechteck einbeschrieben werden, sodass sein Flächenmoment maximal ist

Question

Aufgabe 2:

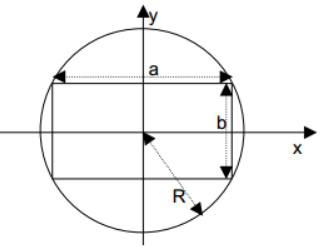
Einem Kreis vom Radius R soll ein Rechteck mit Seitenlängen a und b so einbeschrieben werden, dass sein Flächenmoment $$ I:=\frac{1}{12} a b^{3} $$ maximal ist. Wie groß müssen dazu a und b gewählt werden?

Aufgabe 3:

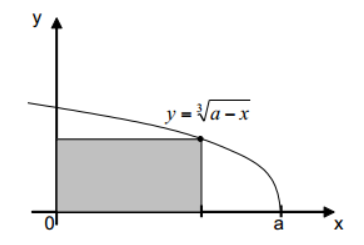
Im 1. Quadranten eines kartesischen Koordinatensystems soll ein Rechteck, wie in der Grafik dargestellt, so zwischen den Koordinatenachsen und der Kurve \( y=\sqrt[3]{a-x} \) \( (\mathrm{a}>0) \) einbeschrieben werden, dass die rechte obere Ecke des Rechtecks auf der Kurve liegt.

Welche Seitenlängen muss das Rechteck haben, damit sein Flächeninhalt maximal ist?

Meine Lösungsansätze:

2.)

a²+b² = 4r²

b² = 4r²-a²

b = √4r²-a²

I_m= (1/12)a * (4r²-a²) ^3/2 // ich habe nun also b³ durch b²*b ersetzt

Bei der Ableitung habe ich dann folgendes raus :

I_m^' = (4r²-a²) ^3/2)/12 - (a² √4r²-a²)/4

Hier ist mein eigentliches Problem, ich kann hierraus keine kritischen Punkte ermitteln.

3.)

F = (a-x)^1/3*x

F^' = x/(3(a-x)^2/3)

Selbes Problem wie bei 2.), obwohl ich hier wohl schon nach 0 auflösen könnte, kommt mir das ziemlich aufwendig vor und ich denke, ich habe vorher schon einen Fehler gemacht?

Answer 1

  hier schon einmal ein erster Ansatz für Frage 2.)
  Da nur nach dem Verhätnis von a zu b gefragt ist
setze ich den Durchmesser d = 1 .

 

Für den Extremwert gilt das der Zähler von I´ gleich null ist.

Leider kommt a = 0.5 und b = 0.866 heraus was derzeit
noch irritirend ist da a laut Skizze größer b sein soll.

Nachtrag : Die denke die Beschriftung der Skizze ist falsch.
I = 1/12 * Breite * Höhe^3
I = 1/12 * b * a^3
dürfte richtig sein.
Es muß aber nur a und b vertauscht werden.

Bei Fehlern oder Fragen wieder melden.

  mfg Georg
 

Comments

Die Lösung wurde mit einem Computerprogramm
gegengeprüft und stimmt.

Bei Fragen wieder melden.

mfg Georg