Wie groß ist die Wahrscheinlichkeit, dass eine Schachtel mehr als 252 g enthält? (Normalverteilung)

Question

Aufgabe:

Das tatsächliche Füllgewicht von Schachteln mit Salz ist eine normalverteilte Zufallsvariable. Der Erwartungswert liegt bei \( 250 \mathrm{~g} \) und die Standardabweichung beträgt \( 25 \mathrm{~g} \).

(Machen Sie bei jeder Aufgabenstellung eine kleine Skizze.)

a) Wie groß ist die Wahrscheinlichkeit, dass eine Schachtel mehr als \( 252 \mathrm{~g} \) enthält?

b) Wie viel Prozent der Schachteln haben ein Gewicht zwischen \( 245 \mathrm{~g} \) und \( 260 \mathrm{~g} \) ?

c) In welchem symmetrisch um den Erwartungswert gelegenen Bereich liegen die Gewichte von \( 60 \% \) aller Schachteln mit Salz?

Ansatz/Problem:

Ich verstehe nicht, wie meine Lehrerin bei c) auf die -0,85 und 0,85 kommt.

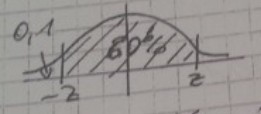
\( \Phi(-z) = 0,2 \\ z = -0,85 \)

\( -0,85=\frac{x-250}{25} \\ x_{1} = 228,75 ~ g\)

\( 0,85=\frac{x-250}{25} \\ x_{2} = 271,25 ~ g\)

Answer 1

40% der Schachteln liegen außerhalb deines gesuchten Intervalls. Da dein Intervall symmetrisch ist, liegen also jeweils links und rechts außerhalb 20%. Du suchst also \(z\) so, dass

\(1) \Phi(-z) = 0,2\) und \( 2)\Phi(z) = 0,8\)

Aus der Tabelle kannst du mit \(2) \) entnehmen, dass \(z = 0,85\).

Aufgrund der Symmetrie (es gilt ja \( \Phi(-z) = 1 - \Phi(z) \)) ergibt sich auch \( \Phi(-0,85) = 0,2 \).

Gruß