Gib eine Funktionsvorschrift der Form f(x) = a·sin(b(x-c))+d an, die die folgende Bedingung erfüllt.

Question

Aufgabe 1:

a. Gib einen Winkel von \( 70^{\circ} \) im Bogenmaß an.

b. Gib ein Bogenmaß von 1,25 (rad) im Gradmaß an.

Aufgabe 2:

Es sei \( f(x)=\sin x \)

a. Der Graph der gesuchten Funktion \( \mathrm{g} \) ist der um 3 Längeneinheiten nach oben verschobene Graph von \( f(x) \).

b. Der Graph der gesuchten Funktion \( g \) ist der an der \( x \)-Achse gespiegelten, in \( y \)-Richtung um 2 gestreckte und um 4 Längeneinheiten nach links verschobene Graph von \( f(x) \).

c. Gib eine Funktionsvorschrift der Form \( f(x)=a \cdot \sin (b(x-c))+d \) an, die die folgende Bedingung erfüllt: Die Wertemenge ist \( [-4 ; 2] \), die Nullstellen sind \( \ldots,-2 \pi,-\pi, 0, \pi, 2 \pi, \ldots \)

Aufgabe 3:

Die Funktion \( g \) ist durch Transformationen aus der normalen Sinusfunktion hervor gegangen.

Gib alle Transformationen an.

a. \( g(x)=4 \cdot \sin (x+5)-6 \)

b. \( g(x)=-0,5 \cdot \sin (3 x-2)-0,6 \)

Aufgabe 4:

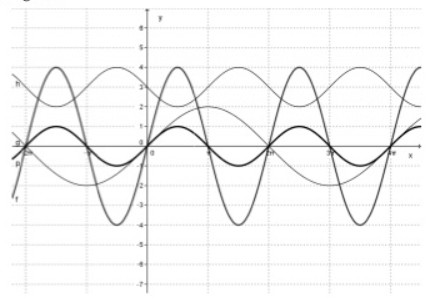
a) Gib zu den Graphen \( f(x) \), \( g(x) \) und \( h(x) \) die zugehörigen Funktionsvorschriften an.

(Orientierungshilfe: \( p(x)= \) \( \sin (x)) \)

b) Beschreibe, wie der Graph von \( g(x) \) aus dem Graphen von \( \mathrm{p}(\mathrm{x}) \) hervorgegangen ist.

Ansatz/Problem:

Wir haben Aufgaben zu den Sinussätzen bekommen, jedoch kann ich Aufgabe 2 und 4 nicht lösen.

Answer 1

2 a) g(x) = SIN(x) + 3

2 b) g(x) = -2 * SIN(x + 4)

2 c) Hier bin ich mir im Unklaren. Die Funktion sollte um -1 nach unten verschoben werden. Dann liegen die Nullstellen allerdings nicht mehr gleichmäßig bei k * pi. Daher denke ich, dass es so eine Funktion nicht geben kann.

4) Ich lasse das mal mit allen Parametern stehen. Normal würde man jetzt noch vereinfachen. Das kannst du selber machen.

f(x) = 4·SIN(1·(x - 0)) + 0

g(x) = 2·SIN(0.5·(x - 0)) + 0

h(x) = -1·SIN(1·(x - 0)) + 3

Beschreibe dann noch wie die Graphen aus p(x) hervorgehen. Gehe dazu kurz auf die allgemeinen Parameter a, b, c und d ein.