Betrachten Sie die Sinusfunktion f(x) = A·sin(B·(x-C))

Question

Aufgabe:

Sei \( x \) eine reelle Zahl und auch \( A, B, C \) reelle Zahlen, wobei \( A \) und \( B \neq 0 . \) Betrachten Sie die Sinusfunktion \( f(x)=A \cdot \sin (B \cdot(x-C)) \) (also die allgemeine Form der Sinusfunktion ohne Verschiebung in \( \mathrm{y} \) -Richtung).

a) Geben Sie die Nullstellen dieser Funktion sowie deren gegenseitigen Abstand an.

b) Wie verändert sich die Amplitude und die Lage sowie der gegenseitige Abstand der Nullstellen dieser Funktion, falls

I. die Parameter A und B verdoppelt werden (C konstant)?
ii. die Parameter A und C halbiert werden (B konstant)?
iii. die Parameter B und C halbiert werden (A konstant)?

c) In welcher der Situationen von Teilaufgabe b) findet eine Stauchung (nzusammendrücken") und wann eine Streckung (nauseinanderziehen") in x-Richtung statt?

Answer 1

Hallo yolo,

die Funktion  f(x) = sin(x)  hat die Nullstellen x_k  =  k·π  mit  k ∈ ℤ (k ist also eine beliebige ganze Zahl).

a)

Für die Nullstellen von  f(x)  =  A · sin( B · (x - C) )  ergibt sich daraus

      B · (x_k - C)  =  k·π     mit  k ∈ ℤ 

⇔   x_k - C  =  k·π /B       mit  k ∈ ℤ

⇔   x_k  =  C + k·π /B      mit  k ∈ ℤ

→→   Der Abstand benachbarter Nullstellen beträgt jeweils π /B

b)   

Der Summand C bewirkt nur eine Verschiebung von g(x) = sin(Bx)  um C nach rechts. C  verändert also die Lage der Nullstellen von f(x), hat aber weder mit der Amplitude noch mit dem Abstand der Nullstellen etwas zu tun.

Die Amplitude ist |A|. A bestimmt also lediglich die maximalen und minimalen Funktionswerte von f(x).

f(x) hat die Periode  p = 2π/B  

	Amplitude	Lage der Nullstellen	Abstand der Nullstellen
A,B verdoppelt	verdoppelt	zwischen je 2 NSt → weitere NS	halbiert
A,C halbiert	halbiert	um C/2 nach links verschoben	unverändert
B,C halbiert	unverändert	jede zweite NST fällt weg + Z3	verdoppelt

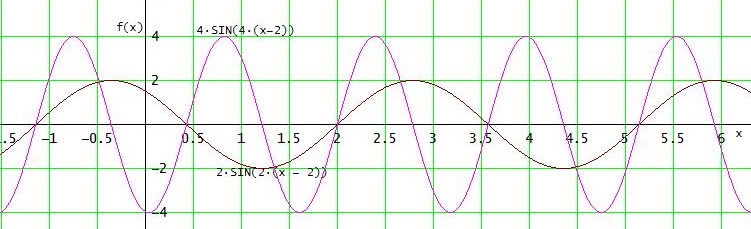
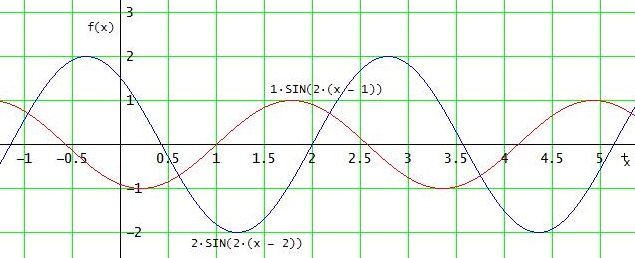
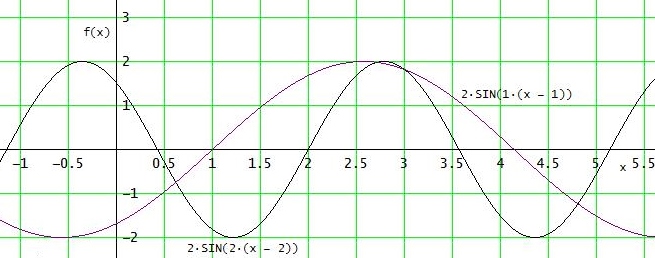
c)

Man hat eine Stauchung bei I und eine Streckung bei III

Gruß Wolfgang

Comments

Genial, danke Wolfgang! :-)