Sorry. Du hast Recht, ich war wohl derjenige, der nicht richtig überlegt hat.
Zur vollständigen Klärung vielleicht Folgendes :
Die „normale“ Sinusfunktion g mit g(x) = sin x verläuft durch den Punkt O = (0|0), hat die Amplitude 1 und die Periodenlänge 2π. Die hier vorliegende Funktion f verläuft hingegen durch den entsprechenden Punkt P = (x0|y0), hat die Amplitude A und die Periodenlänge L.
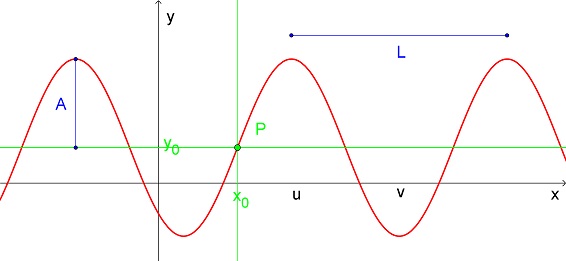
Um nun f(x) = y auf g zurückzuführen, müssen die x-Werte von x0 befreit werden, man wird also x-x0 zu betrachten haben, anschließend muss die Periodenlänge L herausdividiert und die von g hineindividiert werden, das Argument wird also 2π/L*(x-x0). Genau dasselbe trifft auch auf die y-Werte zu : zunächst P auf O bringen indem y-y0 betrachtet wird und dann die Amplitude A herausdividieren und die Amplitude von g (also 1) hineinmultiplizieren führt auf 1/A*(y-y0) = sin(2π/L*(x-x0)). Auflösen nach y liefert den gesuchten Funktionsterm y = f(x) = A*sin(2pi/L*(x-x0))+y0. Häufig wird der Faktor 2π/L mit k abgekürzt (heißt in der Physik „Wellenzahl“), so dass schließlich y = f(x) = A*sin(k*(x-x0))+y0 wird. (Vom Aufgabensteller sind die vier Parameter offenbar mit a,b,c,d bezeichnet worden.)
Sind nun die x-Koordinaten u und v von Hoch- und nachfolgendem Tiefpunkt gegeben, so berechnen sich k und x0 folgendermaßen : Die Periodenlänge ist L = 2*(v-u) und daher k = π/(v-u). Da die Sinusfunktion g einen Hochpunkt an der Stelle π/2 hat, sollte das Argument k*(x-x0) der Funktion f den Wert π/2 annehmen, wenn für x die Stelle u eingesetzt wird : k*(u-x0) = π/2 ergibt 1/(v-u)*(u-x0) = ½ und damit u-x0 = (v-u)/2, also x0 = u - (v-u)/2 = u - L/4