Wie lautet die Gleichung der Tangente und der Normalen? a) f(x) = 1/x^2 – 1 mit B(2|-0.75)

Question

Wie lautet die Gleichung der Tangente und der Normalen im Punkt B an das Schaubild der Funktion f mit :

a) f(x) = 1/x²  – 1 mit B(2|-0.75)

b) f(x) = √x + 2  mit B(9|5)

c) f(x) = 1/x³  – 1 mit B(2|-0.75)

Comments

 

b) f(x) = √x + 2  mit B(9|5)

f ' (x) = 1/2 x^{-1/2} = 1/(2x^{0.5})

mLOT = - 2x_o^{0.5}

Lot: m = 

Gerade durch B

Ansatz: y = mx + q

5 = 9m + q

An der Stelle x_o

(5-q)/9 = m

Beide m gleichsetzen.

-2x_o^{0.5} = (5-q)/9

x_o^0.5 = (q-5)/18

Schnittpunkt

f(x_o) = y_o 

Deshalb:

y_o = mx₀ + q und y_o = x_o^0.5 + 2

 

---

Da B auf der Kurve liegt, gehen a) und b) direkter. Vgl. Antwort Mathecoach.

Bist du sicher, dass bei c) 1/x^3 steht?

So liegt B(2,-0.75) nicht auf der Kurve.

Answer 1

a) f(x) = 1/x² - 1 = x^{-2} - 1 mit B(2|-0.75)

f'(x) = -2x^{-3}
f'(2) = -1/4

t(x) = -1/4 * (x - 2) - 0.75
n(x) = 4 * (x - 2) - 0.75

b) f(x) = √x + 2 = x^{1/2} + 2 mit B(9|5)

f'(x) = 1/2 * x^{-1/2}
f'(9) = 1/6

t(x) = 1/6 * (x - 9) + 5
n(x) = -6 * (x - 9) + 5

Ich multipliziere hier mal die Tangentengleichung und die Normalengleichung nicht aus um zu demonstrieren das man die auch einfach so stehen lassen darf, wenn keine besondere Form gefordert ist.

Hier noch eine Skizze:

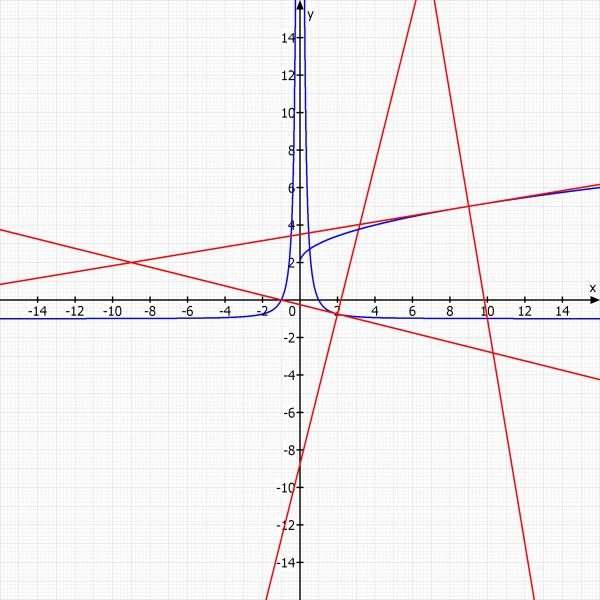
Aufgabe c) solltest du jetzt mal alleine Probieren. 

Wichtig ist nur. Ableitung bilden. X-Koordinate einsetzen und Steigung ausrechnen und dann die Gleichungen in der Punkt-Steigungs-Form aufstellen.