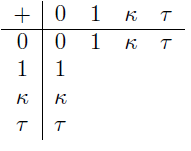Question

In dieser Aufgabe zeigen wir unter der Annahme, dass es einen Körper mit vier Elementen gibt, dass dessen Additions- und Multiplikationstafel eindeutig bestimmt sind.

Sei \(K\) ein Körper mit vier Elementen. Die neutralen Elemente bzgl. Addition und Multiplikation sind dann voneinander verschieden und wir können sie mit 0 und 1 bezeichnen. Die beiden verbleibenden Elementen bezeichnen wir mit \(κ\) und \(τ\).

1) Zeigen Sie, dass dadurch bereits folgende zwölf Einträge der Multiplikationstafel bestimmt sind:

 

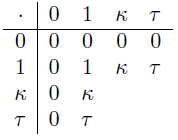
2) Zeigen Sie, dass die verbleibenden vier Einträge der Multiplikationstafel

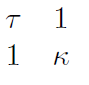
lauten müssen (Tipp: Kürzungsregel für (K*,·)).

3) Zeigen Sie, dass folgende sieben Einträge der Additionstafel bereits feststehen:

Answer 1

also 1) und 3) kommen mir trival vor.

Bei 2) ist es so, dass weder \( \kappa \tau = \tau \) noch \( \kappa \tau = \kappa \) gelten, da daraus \( \kappa = 1 \) oder \( \tau = 1 \) folgen würde. Daher muss \( \kappa \tau = 1 \) sein (und damit \( \tau \kappa = 1 \)).

Wäre \( \kappa^2 = \kappa \), dann wäre \( \kappa (\kappa - 1 ) = 0 \) und damit \( \kappa = 1 = 0 \), ein Widerspruch. Wäre \( \kappa^2 = 1 \), so wäre \( \kappa = \kappa^{-1} = \tau \), ein Widerspruch zu \( \kappa \neq \tau \). Daher muss \( \kappa^2 = \tau \) sein.

MfG

Mister

Comments

Ok, vielen Dank. Die 1) und 2) sind zwar leicht, ich weiss leider nicht so ganz wie ich es erklären könnte. Sollte ich einfach nur die Einträge einzeln nachrechnen? Wie z.B. \(τ+0=τ\) bzw. \(1·0=0\)?

---

Ja, ich würde sie einzeln oder generalisiert nachrechnen.

---

Alles klar dann. Danke

---

mir sind leider die anderen Teilaufgaben auch nicht klar, die aber oben noch nicht erwähnt sind und ich dachte, bevor ich ein neue Frage stelle, mache ich hier einfach mal weiter, da die folgenden Teilaufgaben dazugehören:

1. d)  Begründen Sie die Gleichung 1+κ = κ(1+τ) und führen Sie die Annahmen 1+τ = 0, 1+τ = 1 und 1+τ = τ zum Widerspruch. Schließen Sie daraus auf die vier Einträge 1+κ = κ+1 = τ und τ + 1 = 1 + τ = κ.

2. e)  Zeigen Sie jetzt,dass κ+τ=τ+κ=1.

3. f)  Begründen Sie die noch fehlenden Einträge 1+1 = κ+κ = τ +τ = 0. 

---

Kann ich da vielleicht mit den Körperaxiomen argumentieren?

---

Tut mir leid, ich habe erst jetzt deine Fragen gesehen. Ich weiß auch noch nicht, wie ich es machen werde. Ich werde es mit einem direkten Beweis versuchen, also die Gleichung der Reihe nach zu lösen.

---

Nicht schlimm. Ich habe es auch mit einem direkten Beweis versucht. Mal sehen, ob es stimmt. Werde gleich abgeben. Auflösung gibt es wohl erst nächste Woche in der Übung:)

---

Viel Glück. Ich werde es jetzt versuchen

Answer 2

  Warst du schon mal in der Algebravorlesung? Der Körper mit vier Elementen ist das 2-dimensionale Galoisfeld über dem Primkörper mod 2. Er ist der Zerfällungskörper von

     x ² ^ 2 - x = 0   ( 1 )

      x ^ 4 - x = 0   ( 2 )