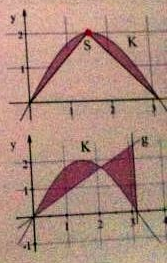Integral: Flächenberechnung eines Rechtecks und Dreiecks über Funktionen

Question

Aufgabe 1:

Der Graph der Funktion f mit f(x) = x(x-3)²; x ∈ ℝ ist K.

1a) H(1|4) ist der Eckpunkt eines Rechtecks, von dem zwei Seiten auf den Koordinatenachsen liegen. K unterteilt das Rechteck in zwei Teile. In welchem Verhältnis stehen die Inhalte der beiden Teilflächen?

1b) K und die x-Achse schließen auf [0, u] für 0 ≤ u ≤ 3 eine Fläche ein. Zeigen Sie, dass für die Maßzahl der eingeschlossenen Fläche gilt: A(u) = 0,25·(u^4 - 8u^3 + 18u^2). Bestimmen Sie die Parallele zur y-Achse, die die Fläche zwischen K und der x-Achse halbiert.

Aufgabe 2:

Gegeben ist die Funktion f mit f(x) = 2 sin x; x ∈ ℝ mit Schaubild K.

2a) Die Abbildung zeigt ein Dreieck, dessen Spitze S auf K liegt. Für welches S sind Dreiecksinhalt und Inhalt der markierten Fläche gleich?

2b) Bestimmen Sie die Gerade g so, dass die beiden Flächen inhaltsgleich sind.

Answer 1

Aufgabe 1a)

f(x) = x·(x - 3)^2 = x^3 - 6·x^2 + 9·x

F(x) = 0.25·x^4 - 2·x^3 + 4.5·x^2

F(1) - F(0) = 11/4 = 2.75

(4 - 2.75) / 2.75 = 5/11

Die Flächen stehen im Verhältnis von 5 zu 11.

Aufgabe 1b)

A(x) = F(x) = 0.25·x^4 - 2·x^3 + 4.5·x^2 = 0.25·(x^4 - 8·x^3 + 18·x^2)

F(3) = 27/4

F(x) = 27/8
0.25·x^4 - 2·x^3 + 4.5·x^2 = 27/8

Hier kommt man mit einem Näherungsverfahren auf

x = 1.157182704

Anbieten tut sich das Newtwonverfahren, da ich ja schon die Ableitung habe.

Aufgabe 2 a)

f(x) = 2·SIN(x)
F(x) = - 2·COS(x)

F(pi) - F(0) = 2 - (-2) = 4

D.h. das Dreieck muss den Flächeninhalt 2 haben.

1/2·pi·(2·SIN(x)) = 2
pi·SIN(x) = 2
x = ARCSIN(2/pi)

x = 0.6901070913
x = pi - 0.6901070913 = 2.451485562

Für S fehlt noch die y-Koordinate. die erhält man durch Einsatz in f(x)

Aufgabe 2 b)

d(x) = 2·SIN(x) - a·x

D(x) = 2·SIN(x) - a·x

D(pi) - D(0) = 0
4 - pi^2·a/2 = 0
a = 8/pi^2 = 0.8105694691

g(x) = 8/pi^2 * x

 
F(1) - F(0) ist die Fläche unter dem Graphen von f im Intervall von 0 bis 1. Da ich F(x) gegeben habe, brauche ich nur einsetzen und zusammenfassen.

Comments

x = ARCSIN(2/pi) was bedeutet diese wort

---

Das ist die Umkehrfunktion von Sinus. Auf dem Taschenrechner SIN^{-1}.

Achte aber darauf das du den Taschenrechner ins Bogenmaß stellen musst.