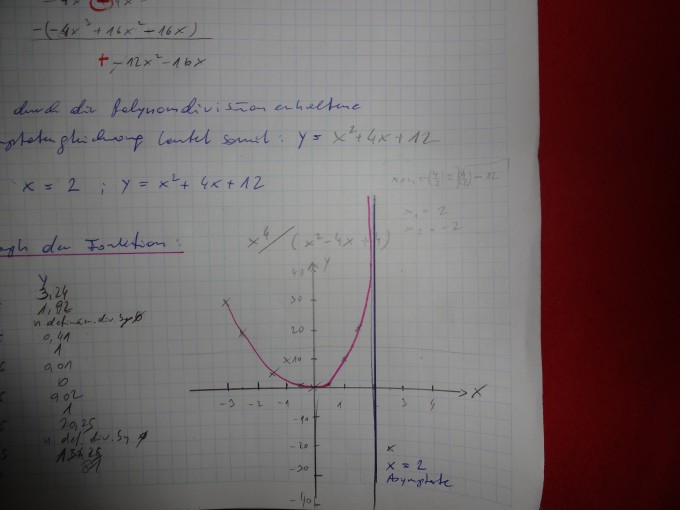
y=(x^4)/(x-2)²
Also ich habe von folgender Funktion die beiden Asymptoten berechnet:
x=2
y=x²+4x+4
R: y=(x^4)/(x-2)²----->x=2 um die Asymptote bei der Polstelle x/0 vorzufinden.
x=2......Asymptotengleichung der Geraden
-------------------------------------
PD:
(x^4) : (x²-4x+4)=x²+4x+12
-(x^4-x^3+4*x^2)
-------------------------------------------
-4*x^3-4*x^2
-(4x^3-16x^2-16*x)
-----------------------------
12*x^2-16*x
Nun habe ich die Funktionswerte in 0,5´er Schritten berechnet:
x/y
-3/3,24
-2,5/1,92
-2/nicht definiert,div.by Null
-1,5/0,41
-1/1
-0,5/0,01
0/0
0,5/0,02
1/1
1,5/20,25
2/nicht definiert,div.by Null
2,5/156,24
3/81
-------------------------------------------------------
die habe ich dann in meine Skizze eingezeichnet aber die Asymptote bei 12 so wie ich meine, oder wo liegt
die, gehört da anscheinend nicht hin:
Ist die y-Asymptote den eine schräge Asymptote, ich kann es mir leider nicht vorstellen??