Also, wenn man sich das Parallelogramm mal in der Ebene vorstellt, dann sind die Verbindungen zwischen A und D sowie zwischen B und C ja parallel und gleich lang. Diesen Sachverhalt machen wir uns zu nutze. D.h. wir verwandeln die Strecke von B nach C in einen Vektor, indem wir vom Ortvektor zu dem Punkt C den Ortsvektor zu dem Punkt B abziehen. Den so gewonnen Vektor addieren wir zu dem Ortvektor von A. Das Ergebnis dieser Summe ist der Ortsvektor zum Punkt D.
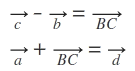
So jetzt du mit Zahlen?!