Aufgabe:
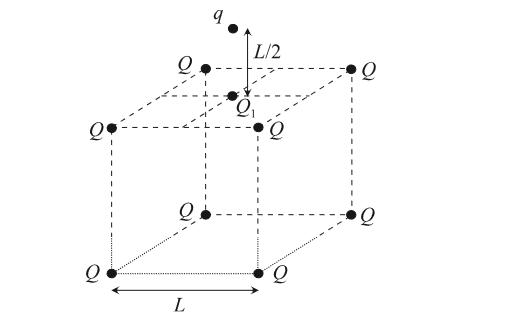
Gegeben ist ein Würfel.
Aber ich weiß nicht, wie die Vektoren von den anderen Punkte Q zu dem Punkt Q1 bestimmt worden sind.
Gibt es bestimmte Methode oder ein einfaches Beispiel?
Exemplarisch:
\( \overrightarrow{a_{1}}=\left(\begin{array}{l} \frac{L}{2} \\ \frac{L}{2} \\ L \end{array}\right) \Rightarrow\left|\overrightarrow{a_{1}}\right|=\sqrt{\left(\frac{L}{2}\right)^{2}+\left(\frac{L}{2}\right)^{2}+L^{2}}=\frac{L \sqrt{3}}{\sqrt{2}} \)
Hinweis: \( \vec{e}_{x}=\frac{1}{|x|} \cdot \vec{x} \)
Es folgt:
\( \vec{F}_{Q_{g e x}, Q_{1}}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q \cdot Q_{1}}{\left(\frac{L \sqrt{3}}{\sqrt{2}}\right)^{2}} \cdot \frac{1}{\frac{L \sqrt{3}}{\sqrt{2}}}\left[\left(\begin{array}{c} \frac{L}{2} \\ \frac{L}{2} \\ L \end{array}\right)+\left(\begin{array}{c} \frac{-L}{2} \\ \frac{L}{2} \\ L \end{array}\right)+\left(\begin{array}{c} \frac{-L}{2} \\ \frac{-L}{2} \\ L \end{array}\right)+\left(\begin{array}{c} \frac{L}{2} \\ \frac{-L}{2} \\ L \end{array}\right)\right] \)