Punkt bestimmen mit Vektoren

Question

Aufgabe:

Die Punkte A(-4|-1|6), B(0|-3|2), C(-2|1|-2) und D(-6|3|2) bilden die Grundfläche einer geraden quadratischen Pyramide mit der Spitze S und der Höhe 9. Die Spitze liegt oberhalb der X₁X₂-Ebene.

a) Geben Sie die Koordinaten von S an.

Problem/Ansatz:

Ich hatte versucht den Verbindungsvektor von A nach C auszurechnen. Davon habe ich dann die Hälfte auf A drauf gerechnet um in die Mitte des Quadrates zu kommen. Dann habe ich die X₃-Koordinate plus 9 gerechnet. Hat nicht so ganz funktioniert :/

Answer 1

Du musst nur entlang des Normalenvektors der Grundfläche gehen. Beachte das die Grundfläche nicht parallel zur xy-Ebene liegt. Daher langt es nicht in z-Richtung zu gehen.

AB = [4, -2, -4]
AC = [2, 2, -8]

Normalenvektor der Ebene

n = [4, -2, -4] ⨯ [2, 2, -8] = [24, 24, 12] = 12·[2, 2, 1]

Mittelpunkt der Strecke AC

F = [-4, -1, 6] + 1/2·[2, 2, -8] = [-3, 0, 2]

Pyramidenspitze S

S = [-3, 0, 2] + 9/|[2, 2, 1]|·[2, 2, 1] = [3, 6, 5]

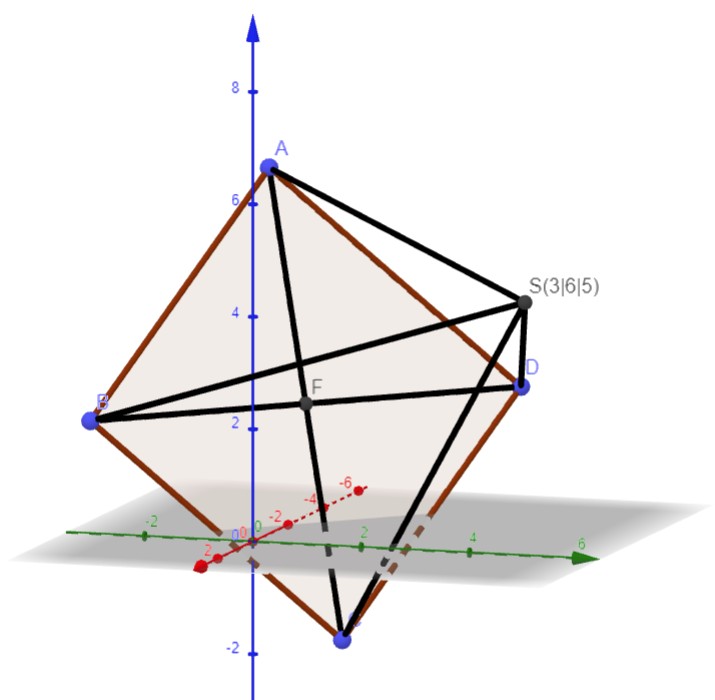
Skizze

Comments

Danke! Aber woher kommt bei F der Vektor [-4,-1,6]?

---

Den Punkt \( F \) erreicht man indem man bei Punkt \(A \) startet und bis zum Mittelpunkt des Vierecks spaziert und \(A \) hat ja gerade die Koordinaten \( \begin{pmatrix} -4\\-1\\6 \end{pmatrix} \).