Folgende Aufgabe versteh ich nicht:
Ein Auto fährt t Sekunden nach dem Beginn einer Beschleunigungsphase annähernd mit der Geschwindigkeit v(t)=3t+15(m/s) Am Beginn dieser Phase ist das Auto 1500m vom Startpunkt entfernt, von dem es sich geradlinig wegbewegt. Wie groß ist seine Entfernung s(t) vom Startpunkt zum Zeitpunkt t?
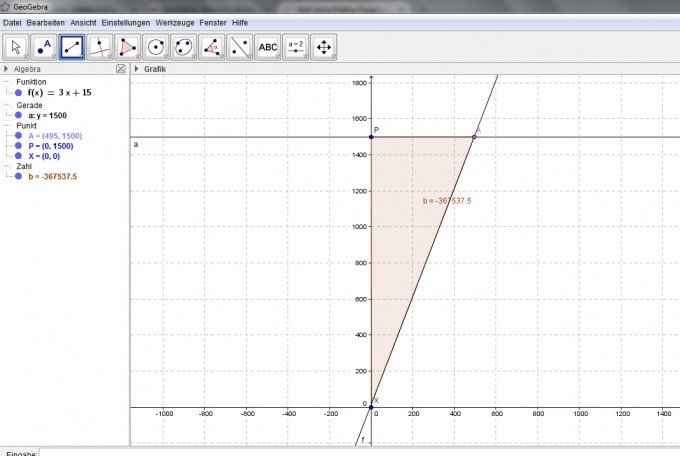
Hab versucht, es mit Geogebra auszurechnen, und dabei eine horrende Zahl gefunden.
Könntet ihr mir weiterhelfen? Mir ist es immer eine große Hilfe, es bildlich betrachten zu können, falls möglich.