Gesucht: ganzrat. achsensym. Fkt. 4. Grades

Question

ich soll eine ganzrationale achsensymmetrische Funktion 4. Grades ermitteln mit den folgenden Eigenschaften:

1. berührt die x-Achse bei x=2

2. Punkt P (0/2) besitzt

jetzt soll ich die Funktionsgleichung angeben.

Wie löse ich die Aufgabe?

heißt berühren Nullpunkt? Ist bei achsensymmetrie auch (-2/0) und (0/-2) ein Punkt? Wenn ja, reichen die 4 Punkte zum lösen?

Vielen Dank vorab?

Answer 1

1) Allgemeine Funktionsgleichung 4. Grades aufstellen

2) Überlegen, welche Terme bei Achsensymmetrie wegfallen

3) Anzahl der Variablen = Anzahl der Bedingungen

4) Bedingungen aufstellen

-------

Jetzt zeige mal, wie weit Du gekommen bist ...

Answer 2

ganzrationale Funktion 4. Grades allgemein:

f(x) = ax⁴ + bx³ + cx² + dx + e

Da die gesuchte Funktion achsensymmetrisch ist, fallen die ungeraden Exponenten weg, so dass sich die Funktion vereinfacht zu

f(x) = ax⁴ + bx² + c

f'(x) = 4ax³ + 2bx

1. berührt die x-Achse bei x=2, also

I. f(2) = 0 = 16a + 4b + c

Da der Funktionsgraph die x-Achse lediglich berührt, aber nicht schneidet, muss dort der Anstieg, also die 1. Ableitung von f(x) = 0 sein, also

II. f'(2) = 0 = 32a + 4b

2. Punkt P (0/2) besitzt

III. f(0) = c = 2

Diese drei Gleichungen kann man in den Taschenrechner eingeben und erhält

a = 0,125

b = -1

c = 2

Damit lautet die gesuchte Funktion

f(x) = 0,125x⁴ - x² + 2

 

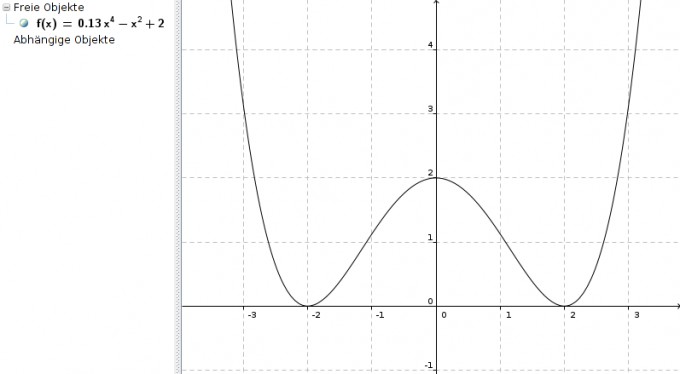
Besten Gruß