In den folgenden Achsenkreuzen sind auf den Achsen die Punkte \( (1,0) \) und \( (0,1) \) durch Striche markiert. Beantworten Sie für jedes der Achsenkreuze die Frage, ob es eine lineare Abbildung
\( F: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2} \)
gibt, die den Vektor \( (0,0) \) auf die durch den Kreis markierte Stelle, den Vektor \( (1,0) \) auf die durch das Kreuz markierte Stelle und den Vektor \( (0,1) \) auf die durch das Kästchen markierte Stelle abbildet.
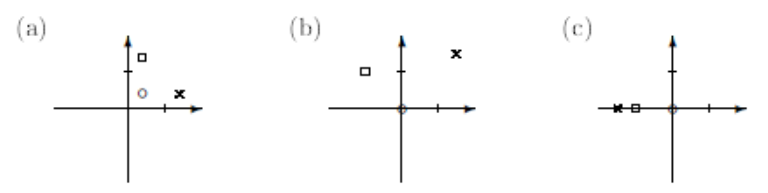
Hinweis: Auch wenn es in dieser Aufgabe nicht auf das genaue Ablesen aus den Achsenkreuzen ankommt, hier die genauen Koordinaten: Bei (a) Kreis \( \left(\frac{2}{5}, \frac{2}{5}\right) \), Kreuz \( \left(\frac{7}{5}, \frac{2}{5}\right) \), Kästchen \( \left(\frac{2}{5}, \frac{7}{5}\right) \), bei (b) Kreis \( (0,0) \), Kreuz \( \left(\frac{3}{2}, \frac{3}{2}\right) \), Kästchen \( (-1,1) \), bei (c) Kreis \( (0,0) \), Kreuz \( \left(-\frac{3}{2}, 0\right) \), Kästchen \( (-1,0) \).