Aufgabe 10:
Mathilda und Emmi machen eine Radtour durch die Berge. Kurz nach Beginn der Radtour lässt sich die zurückgelegte Strecke in km näherungsweise durch die Funktion s mit \( s(t)=(t-3)^{3}+27 \) beschreiben, wobei t für die Stunden seit Messbeginn steht \( (0 \leq t \leq 5) \). Der Graph von s ist abgebildet.
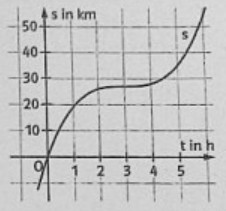
a) Zu welchem Zeitpunkt t seit Messbeginn sind Mathilda und Emmi dem Graphen nach zu urteilen am schnellsten, zu welchem am langsamsten gefahren?
Am schnellsten: _____ Am langsamsten: _____
b) Wie schnell fahren Mathilda und Emmi in den ersten fünf Stunden seit Messbeginn durchschnittlich?
Durchschnittliche Geschwindigkeit: _____
c) Wie schnell fahren Mathilda und Emmi eineinhalb Stunden nach Messbeginn?
Geschwindigkeit nach 1,5 Stunden: _____
d) Wann beträgt die Geschwindigkeit der beiden genau \( 20 \mathrm{~km} / \mathrm{h} \) ? Stelle hierfür zunächst eine entsprechende Gleichung auf.
Ausgangsgleichung: _____ Antwort: _____
Aufgabe 11:
Bäume geben aufgrund der Fotosynthese Sauerstoff an ihre Umgebung ab. Die abgegebene Sauerstoffmenge hängt von der Tageszeit bzw. vom Licht ab. Die Funktion \( V \) mit \( V(t)=-1,2 t^{3}+24 t^{2}+10 t(V(t) \) in \( l \); \( t \) in \( h) \) gibt näherungsweise die Gesamtsauerstoffmenge in Litern an, die ein Baum im Laufe eines Tages nach dem Sonnenaufgang \( (t=0) \) abgibt.
a) Bestimme V'(4). Welche Bedeutung hat V'(4) im Sachzusammenhang?
\( V^{\prime}(4)= \) _____ Bedeutung im Sachzusammenhang: _____
b) Bestimme den Zeitpunkt \( \mathrm{t}_{0} \), für den die Ableitung der Funktion \( \mathrm{V} \) null ist. Interpretiere den Punkt \( \mathrm{P}\left(\mathrm{t}_{0} \mathrm{IV}\left(\mathrm{t}_{0}\right)\right) \) im Sachzusammenhang.(Schränke den Definitionsbereich der Funktion V sinnvoll ein.)
Zeitpunkt: _____
Interpretation im Sachzusammenhang: ____