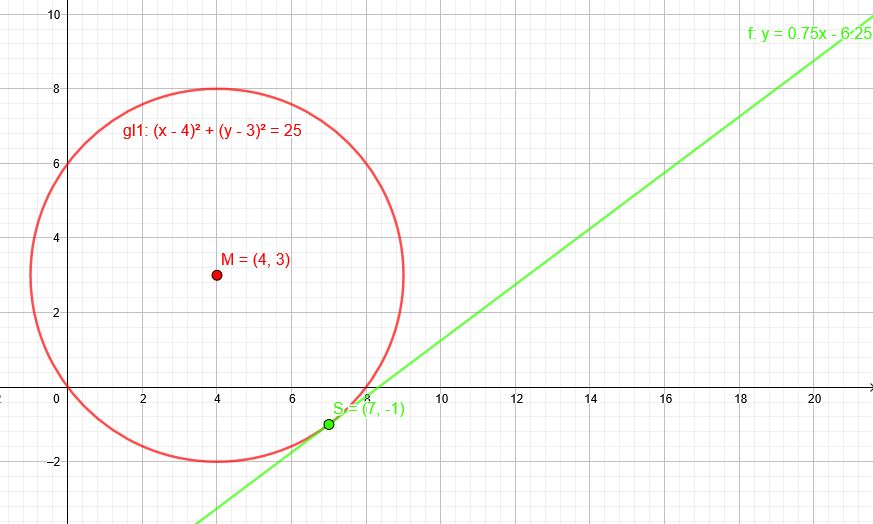
\( (x-4)^2+(y-3)^2=25 \) Punkt auf dem Kreis: \( S(\red{7}|\blue{-1}) \)
\( f(x,y)=(x-4)^2+(y-3)^2-25 \)
\( f_x(x,y)=2\cdot (x-4) \)
\( f_y(x,y)=2\cdot(y-3) \)
\(f'(x)=- \frac{ f_x(x,y)}{f_y(x,y)} \)
\(f'(x)=- \frac{2\cdot (x-4)}{2\cdot(y-3)}=- \frac{x-4}{y-3} \)
\(f'(x)=- \frac{2\cdot (x-4)}{2\cdot(y-3)}=- \frac{\red{7}-4}{\blue{-1}-3}=0,75 \)
Tangente: Nun weiter mit der Punkt-Steigungsform für Geraden.