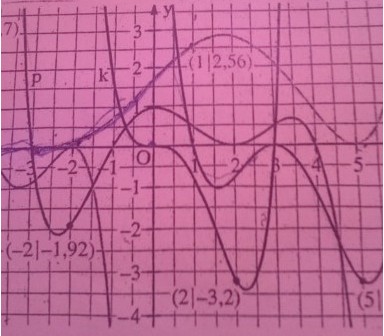
Aufgabe:
Bestimme mit Hife der gezeichneten Graphen die Terme der zugehörigen Funktionen.
Es ist bekannt:
(1) Alle Nullstellen sind ganzzahlig.
(2) Der Grad der Funktion \( f \) und \( p \) ist 5, von \( h \), \( g \) und \( k \) ist 4.
Ansatz/Problem:
Woran erkenne ich am Graphen k bei 0 die dreifache Nullstelle?
Ich soll den Funktionsterm bestimmen, dazu brauche ich die Nullstellen und die Anzahl der Nullstellen.
Da gegeben ist, dass der Graph k vierten Grades ist, aber ich nur 2 einfache Nullstellen gefunden hab, kam mir die frage wie ich eine dreifache Nullstelle am Graphen erkennen kann.