Gleichungssystem: x = a - b·p und x = c + h·p

Question

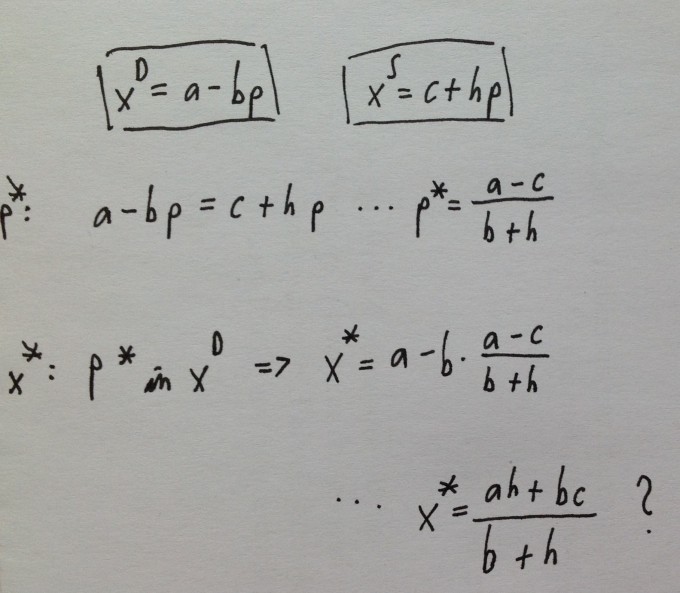
Hallo Forenten,

die eingerahmten Gleichungen sind gegeben, p* und x* sind zu bestimmen.

Wie ich p* bestimme, verstehe ich noch, einfach gleichsetzen.

Um x* zu bestimmen, muss man einsetzen. Allerdings muss die Gleichung dann irgendwie erweitert werden, um auf das Ergebnis zu kommen, und hier liegt mein Problem. Auf diesen Schritt komme ich nicht. :/

Würde mich über Hilfe sehr freuen! :-)

Answer 1

x = a - b·(a - c)/(b + h)

x = a·(b + h) / (b + h) - b·(a - c) / (b + h)

x = (a·(b + h) - b·(a - c)) / (b + h)

x = (a·b + a·h - a·b + b·c) / (b + h)

x = (a·h + b·c) / (b + h)

Comments

Erstmal

Wie genau komme ich denn auf die zweite Zeile? [ a(b+h)/(b+h) ]

Answer 2

a  - b(a-c) / b+h
= a(b+h)/(b+h)    - b(a-c) / b+h  beide auf gl. Nenner !
= (ab+ah -ba++bc )  / (b+h)
=  = (ah ++bc )  / (b+h)

Comments

Erstmal

Wie genau komme ich denn auf die zweite Zeile? [ a(b+h)/(b+h) ]

---

Willst du Bruch zu Bruch addieren,

Bruch von Bruch gar subtrahieren,

musst du sie vor allen Dingen,

auf den gleichen Nenner bringen :)

Das geeignete Stichwort heißt hier Erweitern.

a = a / 1 = a·(b + h) / (b + h)

---

Manchmal steht man total auf dem Schlauch.

Danke Dir / Euch für die Erklärungen.