ich habe die dichte eines Drahtstücks das zwischen den koordinaten (-2,0) und (2,0) liegt. wie berechne ich die Masse?

Question

Also um erlich zu sagen, ich kapiere wie ich das drahtstück zeichnen muss (das ist nicht so schwer), und die berechnung der masse ist nicht schwer. Ich verstehe nur nicht was ich unter (a) machen soll. Was meint er mit "kennzeichne in der Skizze an 5 beliebigen stellen die Dichte)"

ALSO, so wie ich das begriffen habe, so soll das Drahtstück im koordinaten system aussehen. Wie soll ich jetzt da die dichte kennzeichnen.

Comments

Ich verstehe die Aufgabe auch nicht.
Aber muß nicht dein oberster Punkt bei ( 0 | 2 ) liegen ?

---

ja, ich weis, ich konnte es nicht bei genau 2 landen lassen. aber trotzdem. man kapiert was ich sagen will (oder?)

Answer 1

Hm. Das soll ein Halbkreis mit dem Radius 2 sein. Also Nullstellen bei -2 und +2 und y-Achsenabschnitt bei 2.

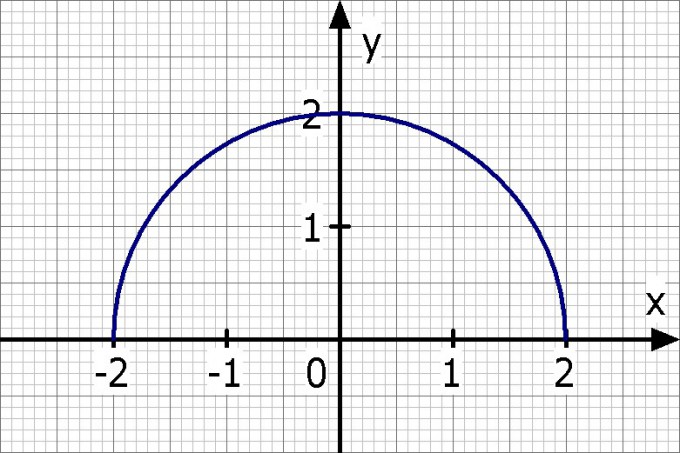
Und dann sollst du auf dem Halbkreis 5 Punkte markieren und dazu die Dichte ermitteln.

[x, √(2^2 - x^2), √(2^2 - x^2) + 1
-2, 0, 1;
-1.5, 1.322875655, 2.322875655;
-1, 1.732050807, 2.732050807;
-0.5, 1.936491673, 2.936491673;
0, 2, 3;
0.5, 1.936491673, 2.936491673;
1, 1.732050807, 2.732050807;
1.5, 1.322875655, 2.322875655;
2, 0, 1]

Hier wurde einfach nur y und rho durch x ausgedrückt und berechnet. Das Gewicht des Drahtes kann mit der Funktion aber auch Geschickterweise über Polarkoordinaten berechnet werden. Also

[x, 2·COS(x°), 2·SIN(x°), 2·SIN(x°) + 1;
0, 2, 0, 1;
15, 1.931851652, 0.5176380902, 1.517638090;
30, 1.732050807, 1, 2;
45, 1.414213562, 1.414213562, 2.414213562;
60, 1, 1.732050807, 2.732050807;
75, 0.5176380902, 1.931851652, 2.931851652;
90, 0, 2, 3;
105, -0.5176380902, 1.931851652, 2.931851652;
120, -1, 1.732050807, 2.732050807;
135, -1.414213562, 1.414213562, 2.414213562;
150, -1.732050807, 1, 2;
165, -1.931851652, 0.5176380902, 1.517638090;
180, -2, 0, 1]

Beide Ansätze führen uns auf ein Drahtgewicht von ca. 14.28 g.

Comments

ja, das verstehe ich. aber wie markiere ich die 5 punkte??

---

Der Fragesteller soll also :
ein x willkürlich festlegen,
das y dazu ausrechnen
und dann die Dichte über
rho  = y + 1 in g / cm^2 berechnen ?

---

also, einfach irgendein punkt wehlen (bsp: 1.5|1.75) dann die Y koordinate wehlen und die dichte = y+1 = 2.75 g/cm³ berechnen??? und das noch 4 mall??

---

also, einfach irgendein punkt wehlen (bsp: 1.5 | 1.75 ) 
y = √ ( 2² - x² )
y = √ ( 2² - 1.5² )
y = 1.32

dann die Y koordinate wehlen
Haben wir bereits berechnet y = 1.32

und die dichte = y+1 = 1.32 + 1 = 2.32 g/cm³ berechnen???
und das noch 4 mall??

Denke schon.

---

ja aber (warte, vielleicht spreche ich idiotismus aber trotzdem) ist nicht: X² + y² = 4 ein kreis?????

Der draht formt ein halfkreis.

---

ja also

X² + y² = 4

y >= 0

Halbkreis !

---

Der obere Halbkreis hat die Formel
y = + √ ( 2² - x² )
der untere Halbkreis hat die Formel
y = - √ ( 2² - x² )

mfg Georg

---

Ich habe mal meine Antwort oben erweitert. Weil das Berechnen der Punkte über die Kreisgleichung auf einen komplizierteren Weg zur Berechnung des Drahtgewichts führt.

---

hallo Mathcoach,
abgesehen vom mathematischen kann ich mir die ganzen Gegebenheiten
nicht vorstellen.
Ein im Halbkreis gebogener Draht. Noch verstanden.
Aber welchen Querschnitt hat der Draht. Kreis, Aber welcher Durchmesser ?

---

Kein Durchmesser und und kein Querschnitt. Wir haben eine Punktelinie. Aber jeder Punkt hat eine Dichte.

Die Dichte ist daher auch in g/cm und nicht etwa in g/cm³ angegeben.

Wenn man also einen Draht mit einer Länge von pi * 2 = 6,283 cm hat mit einer Dichte von 1 dann hat man 6.283 g. Wenn man nun eine Dichte von 3 hat, dann ist das Gewicht 18.85 g. Da die Dichte hier nicht konstant ist erwarten wir also einen Wert zwischen 6.283 g und 18.85 g.

Answer 2

y = √ ( 2^2 - x^2 )

rho ( y ) = y + 1
rho ( x ) =  √ ( 4 - x^2 ) + 1

x = 1
rho ( 1 ) =  √ ( 4 - 1^2 ) + 1
rho =  2.732 gr / cm^2

b.)
∫ rho ( x ) dx zwischen -2 und 2

Soweit meine Überlegungen.

Comments

Hi, zu b): Muss es denn nicht ein mit der Dichte gewichtetes Wegintegral über den Halbkreis sein?

---

@jf116: Ja, das sollte es. Wenn ich PhoenixOroboros aber richtig verstanden habe ist die Massenberechnung eh kein Problem gewesen. Er wußte nur nicht wie er Punkte auf der Kurve angeben sollte und zu den Punkten die Dichte berechnnen sollte.

---

Ich muss auch diese Aufgabe rechnen.

Ich hab jetzt zu b das Integral von rho (x) berechnet und das mit der Länge des Drahtes (welche ich durch die formel für die bogenlänge berechnet habe) multipliziert.

Darf man das so machen?

Komme dann auf ein Ergebnis von 64,61 g  was mir etwas viel vorkommt......

---

Das ist so auch verkehrt. Du musst über alle infinitisimal kleinen Gewichte des des Drahtes integrieren.

---

"und die berechnung der masse ist nicht schwer"

Vielleicht lässt euch PhoenixOroboros ja an seiner Rechnung mal teilhaben.

Ich komme zur Kontrolle auf: 14.28 g

---

das heißt ich berechne das integral von rho (x).

da habe ich 2pi+4 raus ......soweit okay?

aber wie mach ich dann weiter?

---

Die Masse des Drahtes bekommt man als Kurvenintegral: \(\int_C\rho(x,y)\,ds\). Hier ist \(C\) der obere Halbkreis. Es handelt sich schliesslich um eine lineare Dichte, d.h. \(dm=\rho\,ds\). Das Integral rechnet man ueber Polarkoordinaten aus.