Um das Volumen des Prisma zu berechnen braucht man die Grundfläche , die Grundfläche hierfür ist ein Trapez
VPrisma=G*h
GTrapez=m*hTrapez ,m=1/2*(a+c)
gegeben ist a=12cm, c=7cm hTrapez=4cm und hPrisma=12
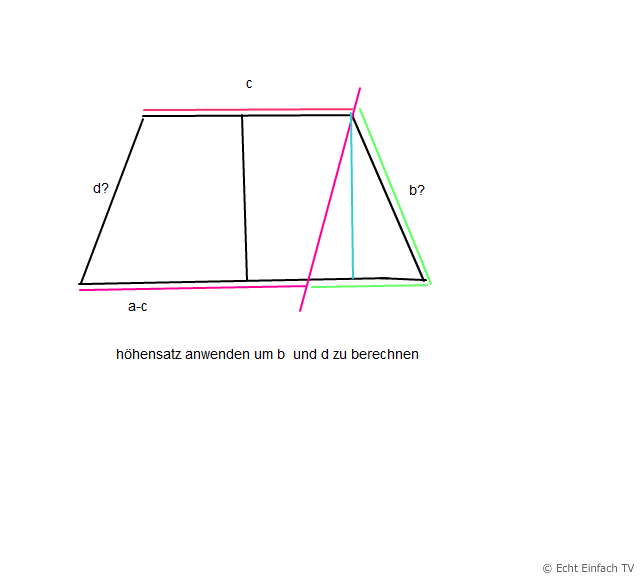
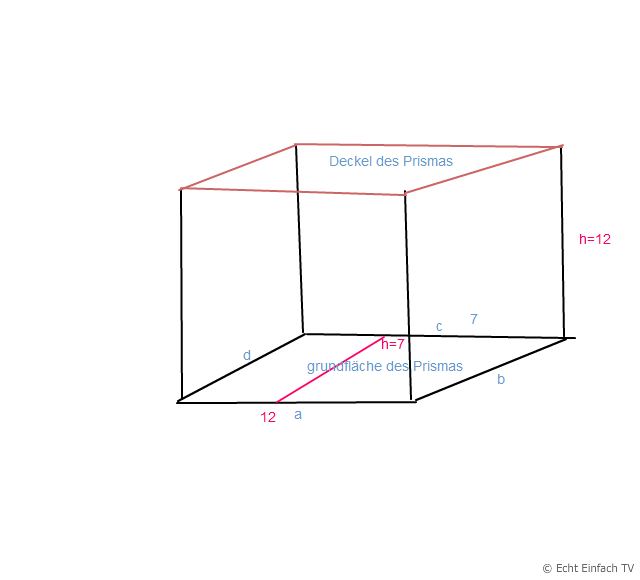
Um die Oberfläche des Prismas zu ermitteln, braucht man auch noch die Seiten b und d von der Grundfläche GTRapez, und in der Tat macht es Sinn, die beiden bekannten Seiten voneinander zu subtrahieren, um auf die fehlenden Längen der beiden gesuchten Seiten zu kommen.
Oprisma=2*G+M M=a*h+b*h+c*h+d*h hier ist die Höhe des Prismas einzusetzen.