Beweis \binom{2k}{k}/2^{2k}

Question

Hallo Forum Mitglieder,

irgendiwe schaffe ich es nicht folgendes zu beweisen:

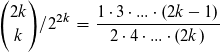
Ich habe schon mal versucht das ganze umzuformen und bis bis hierhin gekommen:

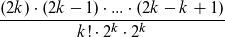
Wiel ja 2^k * k! eigentlch schon 2*4*...*(2k) ergeben müssten, muss ich nur noch das andere 2^k wegkürzen, aber wie?

LG

Orbi

Answer 1

also du brauchst eigentlich nur das hier https://de.wikipedia.org/wiki/Fakult%C3%A4t_(Mathematik)#Doppelfakult.C3.A4t (der Link wird wegen des Unterstrichs falsch dargestellt. Beim Wikipediaartikel zum Thema "Fakultät" einfach der Unterpunkt "Doppelfakultät" suchen) zum Thema Doppelfakultät. Mit den dort angegebenen Formeln erhältst du

$$\begin{pmatrix}2k \\ k\end{pmatrix} / 2^{2k} = \frac{(2k)!}{k!\ k! \ 2^{2k}} = \frac{(2k)!}{(k! \ 2^k)^2} = \frac{(2k-1)!!}{k! \ 2^k} = \frac{(2k-1)!!}{(2k)!!}$$

$$= \frac{1 \cdot 3 \cdot ... \cdot (2k-1)}{2 \cdot 4 \cdot ... \cdot 2k} \ .$$

Comments

Wow, das  mit der Doppelfakultät hatten wir noch gar nicht in der Vorlesung, ist aber ziemlich interessant und nützlich! Vielen Dank Yukawah! Kann man die Formel denn nicht auch mit anderen Mitteln umformen?

---

Die Doppelfakultät steht einfach nur für einen bestimmten Ausdruck. Wenn ihr das in der Vorlesung nicht habt ersetz die Doppelfakultät einfach durch den entsprechenden Ausdruck und gut ist.