allo, ich hatte gestern meine mündliche Abitur Prüfung und ich bin entsetzt, weil die Prüfer ganz Offensichtlich einen Fehler gemacht haben. Ich brauche euer Rat !
In der Bubu Liga gibt es drei Fußballvereine, der Fc Saum (S), der Fc Kellingen K und der Fc Tür T. Innerhalb eines Jahres wechseln einige Spieler den Verein und einige bleiben bei ihrem Club. Der Verein wechsel wird in dem folgenden Diagram beschrieben.
Ich habe mithilfe vom dem Diagram eine Übergangsmatrix erstellt
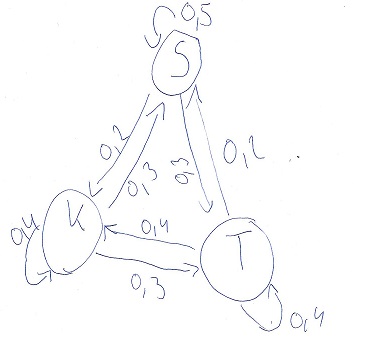

und dann habe ich die information in die formlel
M mal xvektor = xvektor
so sieht die gleichung aus
0,5x1 + 0,3x2 + 0.2x3 = x1
0,2x1 +0.4x2 +0.4x3 = x2
0.3x1 + 0.3x2 + 0.4x3 =X3
ich habe ( x1,x2,x3) von rechts nach links verschoben, also kommt folgendes raus
1) -0,5x1 + 0,3x2 + 0.2x3 = 0
2) 0,2x1 -0.6x2 +0.4x3 = 0
3) 0.3x1 + 0.3x2 - 0.6x3 = 0
Dann habe ich per Gaußverfahren die Gleichung aufgelöst und kam
auf diese Matrix
1 1 -2 0
0 2 -2 0
0 0 0 0
also
x1 + x2 - 2x3 = 0
2x2 - 2x3 = 0
0= 0
also
0= 0 also kommt hier folgendes raus x3 = x3
2x2 - 2x3 = 0 hier nach x2 auflösen hier kommt folgendes raus x2 = x3
x1 + x2 - 2x3 = 0 hier setze ich x2 ein hier kommt folgendes raus x1 = x3
also ist der fixvektor = (x3,x3,x3) wenn man x3 auflösen möchte dann = x3 (1,1,1)
ist x3 intressiert uns nicht
also ist unsere Fixvektor = (1,1,1)
Aber die Prüfer meinten der Fixvektor sei falsch, weil die spaltensumme vom fixvektor eins ergeben muss, weil wir eine stochastische Matrix haben,
Bitte helft mir ist der Fixvektor wirklich falsch, ich fühle mich ungerecht behandelt.