Ahoi,
Ich hänge an ner Aufgabe und möchte gerne wissen, ob es mit der Lösung von mir seine Richtigkeit hat. Die Aufgabe hat das Pascalsche Dreieck zum Thema und lautet
$$\quad \quad (\sqrt { a } -\frac { 1 }{ \sqrt { a } } { ) }^{ 6 }$$
und meine Lösung dazu, etwas ausführlicher, denn ich bin mir eigentlich sicher das etwas nicht stimmt aber ist ja schon etwas spät :D:D
$$\quad \quad (\sqrt { a } -\frac { 1 }{ \sqrt { a } } { ) }^{ 6 }\\ =1\sqrt [ 2 ]{ { a }^{ 6 } } (-\frac { 1 }{ \sqrt [ 2 ]{ a^{ 0 } } } )+6\sqrt [ 2 ]{ { a }^{ 5 } } (-\frac { 1 }{ \sqrt [ 2 ]{ { a }^{ 1 } } } )+15\sqrt [ 2 ]{ { a }^{ 4 } } (-\frac { 1 }{ \sqrt [ 2 ]{ { a }^{ 2 } } } )+20\sqrt [ 2 ]{ { a }^{ 3 } } (-\frac { 1 }{ \sqrt [ 2 ]{ { a }^{ 3 } } } )+15\sqrt [ 2 ]{ { a }^{ 2 } } (-\frac { 1 }{ \sqrt [ 2 ]{ { a }^{ 4 } } } )+6\sqrt [ 2 ]{ { a }^{ 1 } } (-\frac { 1 }{ \sqrt [ 2 ]{ { a }^{ 5 } } } )+1\sqrt [ 2 ]{ { a }^{ 0 } } (-\frac { 1 }{ \sqrt [ 2 ]{ { a }^{ 6 } } } )\\ ={ a }^{ \frac { 6 }{ 2 } }(-\frac { 1 }{ { a }^{ \frac { 0 }{ 2 } } } )+{ 6a }^{ \frac { 5 }{ 2 } }(-\frac { 1 }{ { a }^{ \frac { 1 }{ 2 } } } )+{ 15a }^{ \frac { 4 }{ 2 } }(-\frac { 1 }{ { a }^{ \frac { 2 }{ 2 } } } )+{ 20a }^{ \frac { 3 }{ 2 } }(-\frac { 1 }{ { a }^{ \frac { 3 }{ 2 } } } )+{ 15a }^{ \frac { 2 }{ 2 } }(-\frac { 1 }{ { a }^{ \frac { 4 }{ 2 } } } )+{ 6a }^{ \frac { 1 }{ 2 } }(-\frac { 1 }{ { a }^{ \frac { 5 }{ 2 } } } )+{ 1 }a^{ \frac { 0 }{ 2 } }(-\frac { 1 }{ { a }^{ \frac { 6 }{ 2 } } } )\\ ={ a }^{ \frac { 6 }{ 2 } }(-({ a }^{ { - }^{ \frac { 0 }{ 2 } } }))+{ 6a }^{ \frac { 5 }{ 2 } }(-({ a }^{ { - }^{ \frac { 1 }{ 2 } } }))+{ 15 }a^{ \frac { 4 }{ 2 } }(-({ a }^{ { - }\frac { 2 }{ 2 } }))+{ 20a }^{ \frac { 3 }{ 2 } }(-({ a }^{ { - }^{ \frac { 3 }{ 2 } } }))+{ 15 }a^{ \frac { 2 }{ 2 } }(-({ a }^{ { - }^{ \frac { 4 }{ 2 } } }))+{ 6a }^{ \frac { 1 }{ 2 } }(-({ a }^{ { - }^{ \frac { 5 }{ 2 } } }))+{ 1a }^{ \frac { 0 }{ 2 } }(-({ a }^{ { - }^{ \frac { 6 }{ 2 } } }))\\ ={ a }^{ \frac { 6 }{ 2 } }(-1)+(-6{ a }^{ \frac { 5 }{ 2 } +(-\frac { 1 }{ 2 } ) })+(-15a^{ \frac { 4 }{ 2 } +(-\frac { 2 }{ 2 } ) })+{ (-20a }^{ \frac { 3 }{ 2 } +(-\frac { 3 }{ 2 } ) })+{ (-15 }a^{ \frac { 2 }{ 2 } +(-\frac { 4 }{ 2 } ) })+(-{ 6a }^{ \frac { 1 }{ 2 } +(-\frac { 5 }{ 2 } ) })+(-{ 1a }^{ \frac { 0 }{ 2 } +(-\frac { 6 }{ 2 } ) })\\ =-{ a }^{ 3 }-6{ a }^{ 2 }-15a-20-15\frac { 1 }{ a } -6\frac { 1 }{ { a }^{ 2 } } -{ a }^{ 3 }\quad \quad ??$$
oder nochmal als Bilddatei, ich habe wo ich die Vorzeichen herleite rot markiert...
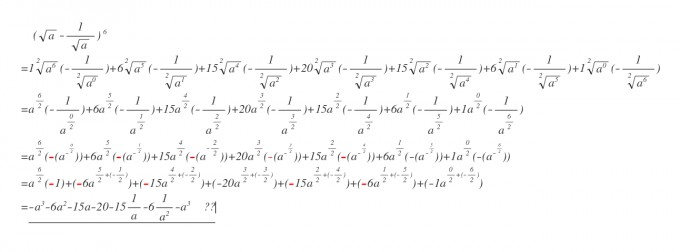
Ich danke euch im voraus und verbleibe
Salut