Ich versuche es einmal ohne Skizze.
Bitte einmal ein rechtwinkliges Dreieck aufmalen und die Seiten mit
a,b Katheten und c Hypotenuse beschriften und
den rechten Winkel markieren.
Fläche A = a * b / 2 = 1
c^2 = a^2 + b^2
U = a + b + c ( min und max sind gesucht )
a * b / 2 = 1
b = 2 / a
c = √ ( a^2 + b^2 )
c = √ ( a^2 + ( 2 / a )^2 )
U = a + 2 / a + √ ( a^2 + ( 2 / a )^2 )
1.Ableitung nach a bilden und für die Extremwerte
zu 0 setzen und a berechnen. Alles andere ergibt sich dann.
Leider kommt bei der 1.Ableitung ein Lindwurm heraus. a = √ 2
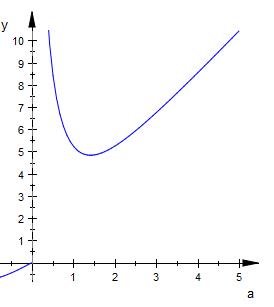
Hier noch die Skizze