Zunächst einmal würde ich dir empfehlen, das Dreieck zu zeichnen. Dies kannst du z.B. mit einem Zirkel machen (ich nehme mal an, du weißt wie das funktioniert).
Das Dreieck könnte dann ungefähr so aussehen:
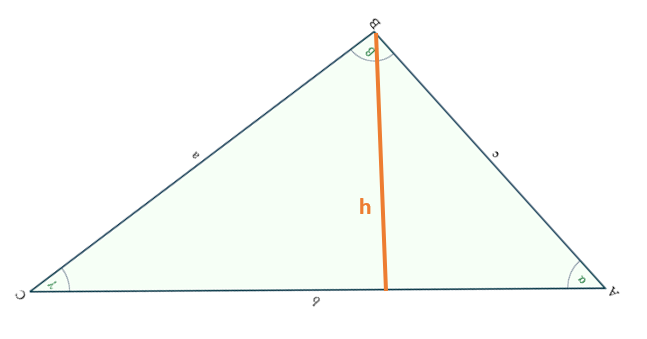
Für den Flächeninhalt eines Dreiecks gilt: A=\( \frac{g·h}{2} \).
unser g wäre in diesem Fall b=20. Gesucht ist nun die höhe h. Diese kann man berechnen mit sin α=\( \frac{Gegenkathete}{Hypotenuse} \). α≈48,35°, Gegenkathete=h, c=12.
Dann erhalten wir:
sin (48,35)=\( \frac{h}{12} \) | ·12
⇔ sin (48,35)·12=h
⇔ h≈8,97.
A=\( \frac{20·8,97}{2} \)=89,6. Der Flächeninhalt des Dreiecks beträgt also 89,6cm2.
Berechnen Sie den Umfang jenes Quadrats, das den gleichen Flächeninhalt hat
Für den Umfang eines Quadrats gilt: U=4a. Um a zu bestimmen löst man a2=89,6 nach a auf, indem man die Wurzel zieht.
a=\( \sqrt{89,6} \) ⇔ a≈9,47cm. U=4·9,47=37,88cm. Der Umfang jenes Quadrats, das den gleichen Flächeninhalt hat, beträgt 37,88cm
Berechnen Sie den Flächeninhalt jenes Kreises, welcher den gleichen Umfang wie das Dreieck hat.
Umfang des Dreiecks: 20cm+12cm+15cm=47cm.
Umfang vom Kreis: U=2·π·r. Es folgt die Gleichung:
2·π·r=47cm | ÷2π
⇔ r≈7,48cm.
Flächeninhalt vom Kreis: A=π·(7,48cm)2 ≈23,5cm2