Knobelaufgabe: Kreis und Quadrat

Question

Aufgabe:

Die Seitenlänge des Quadrats beträgt 10cm. Vergleiche den Umfang des Quadrats mit dem des Kreises.

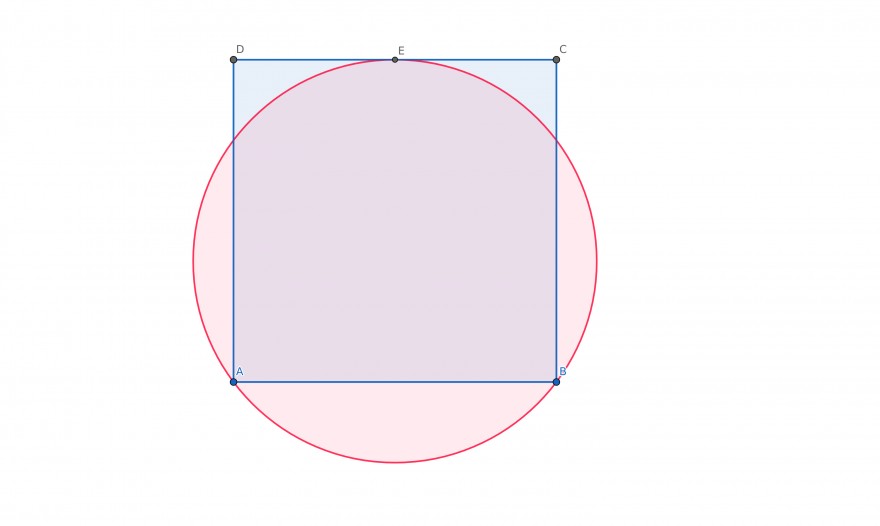
Problem/Ansatz:

Ich habe die Aufgabe bereits gelöst, finde sie aber so interessant, dass ich sie euch nicht vorenthalten möchte. Es gibt verschiedene Lösungswege. Wer findet den elegantesten? :-)

PS:

Die bisherigen Antworten zeigen, wie unterschiedlich so ein Problem gelöst werden kann. Ich persönlich hatte es mit dem Höhensatz bearbeitet.

Mir fällt es schwer, eine Lösung als beste Antwort zu kennzeichnen, da alle sehr kreativ sind.

Comments

Thales erlaubt die Anwendung des Kathetensatzes :  AE^2  =  EF * EH

Text erkannt:

.0
\( \mathbf{c} \)
:

Somit wird  d  =  EF  =  AE^2 / EH  =  ( (a/2)^2 + a^2 ) / a  =  a/4 + a  =  5/4 * a

Alternative :  im ΔAHE ist die kurze Kathete halb so lang wie die lange, das muss also auch im dazu ähnlichen ΔFHA gelten :  FH = 1/2 * AH = 1/4 a , d = 5/4 a

---

Meine Lösungsskizze sieht genau so aus. :-)

Allerdings habe ich den Höhensatz verwendet, um die Strecke HF zu bestimmen.

---

Die Aufgabe war schon mal dran. hj hatte damals aber auch 'nur' die 'klassische' Lösung vom Mathecoach gepostet.

Btw.: die Alternativlösung von hj finde ich am besten.

Answer 1

(a - r)^2 + (a/2)^2 = r^2 --> r = 5/8·a

UK / UQ = (2·pi·5/8·a)/(4·a) = 5/16·pi = 0.9817

Der Umfang des Kreises ist 5/16·pi mal so groß wie der Umfang des Kreises.

Answer 2

Schöne Aufgabe !

dazu folgende Skizze:

Das Quadrat \(ABCD\) habe die Seitenlänge \(a\) und der Kreis um \(M\) den Durchmesser \(d\). Streckt man \(ABCD\)  ausgehend von \(Z\) zu \(A'B'C'D'\) so erhält man ein neues Quadrat mit der Seitenlänge \(d\). \(M_a'\) und \(M_b'\) sind die Mittelpunkte der Seiten \(A'B'\) und \(B'C'\). 

Die Mittelparallele des Dreiecks \(\triangle A'B'M_b'\) schneidet \(ZB'\) in \(B\), da der Kreis Thaleskreis über \(ZM_a'\) ist. Daraus folgt, dass \(|PB| = |BB'|\) (rot). Die durch die Geraden \(ZB'\) und \(A'M_b'\) entstandenen rechtwinkligen Dreiecke haben offensichtlich alle ein Kathetenverhältnis von \(1:2\). Daraus folgt u.a. \(|BB'| = |PM_b'|\) (rot) und damit ist auch \(|A'P| = |ZB|\) (grün).

Man erhält dann aus dem Kathetenverhältnis von \(\triangle A'B'P\) $$\frac {|A'P|}{|PB'|} = \frac{|ZB|}{2|BB'|} = 2  \implies |ZB| : |BB'| = 4 : 1 \\ \implies |ZB| : |ZB'| = 4 : 5 $$und da bei einer zentrischen Streckung alle Streckenverhältnisse gleich sind, ist auch \(a : d = 4 : 5\) bzw. \(d = \frac 54 a\)$$\implies \frac{U_Q}{U_K} = \frac{4a}{\frac 54 a \pi} = \frac {16}{5 \pi}$$