Runge-Kutta Verfahren, AWP Hilfe

Question

ich weiß leider gar nicht wie man hier anfangen soll, kann mir da bitte jemand helfen?

LG und einen schönen Abend!

Comments

Schreib doch mal die Formeln für das Euler- und das Runge Kutta Verfahren hin. Dann sieht man weiter.

---

Ich weiß nicht so genau, bin gerade etwas überfordert ..

---

Aber wenn Du die Formeln nicht kennst, wie willst Du denn so ein Problem lösen? Schau mal hier

https://de.wikipedia.org/wiki/Explizites_Euler-Verfahren

https://de.wikipedia.org/wiki/Runge-Kutta-Verfahren

da steht doch alles.

---

Sind das die Formeln für das explizite Euler-Verfahren und das für Runge Kutte Verfahren?

Answer 1

Also in dem Link steht doch folgendes. Die Dgl.

$\dot x(t) = f(t,x(t))$ mit $x(t_0) = x_0$ wird durch das Eulerverfahren wie folgt gelöst

$x_{k+1} = x_k + h f(t_k,x_k)$ wobei $t_k = t_0 + kh$ gilt.

In Deinem Fall ist $t_0 = 0$, $h = 1$, $x_0 = 1$ und $f(t,x) = t + x$

Die Lösung der Dgl. ist $x(t) = 2 e^t - t - 1$ wie man durch nachrechnen bestätigen kann

Die ersten Werte für $x_k$ sind die folgenden. $x = \begin{pmatrix} 1 \\ 2 \\ 5 \\ 12 \\ 27 \\ 58 \end{pmatrix}$

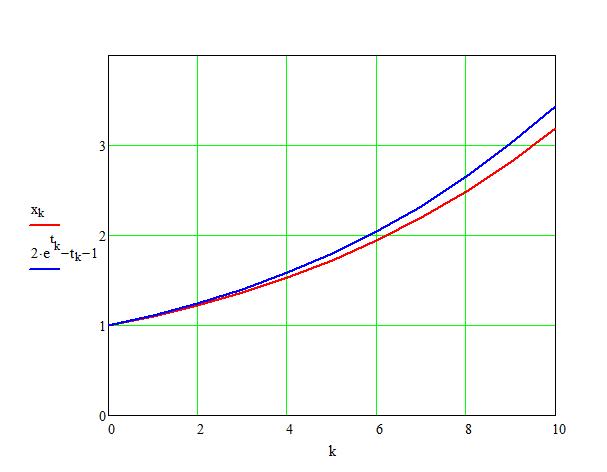
Der Vergleich mit der tatsächlichen Lösung sieht so aus

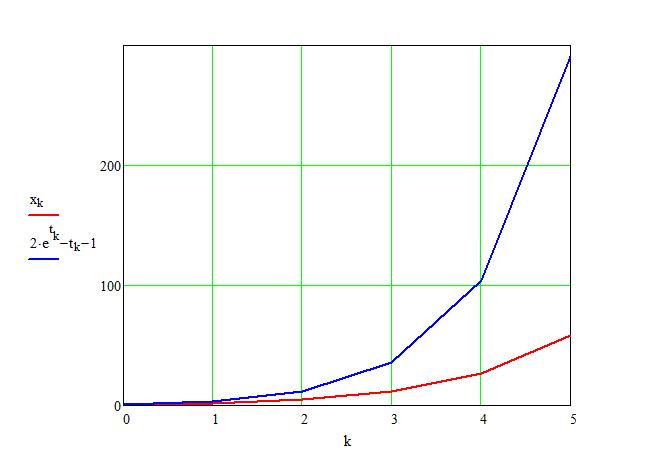Wie man sieht, gibt es erhebliche Abweichungen zwischen der numerischen und der exakten Lösung. Diese Abweichung kann man durch Reduktion der Schrittweite $h$ vermindern.

Und so sieht die numerische Lösung mit einer Schrittweite von $h = 0.1$ aus.

Comments

Und jetzt das Runge-Kutta Verfahren für $h = 1$. Man sieht, dass das Runge-Kutta Verfahren deutlich besser ist als das Euler Verfahren. Zwischen der numerischen Lösung und der exakten ist trotz der groben Schrittweite kaum ein unterschied zu sehen.