Reihen Konvergenz und Divergenz bei Fallunterscheiden zeigen...

Question

Hallo Forum-Mitglieder,

cih habe folgende Reihe gegeben:

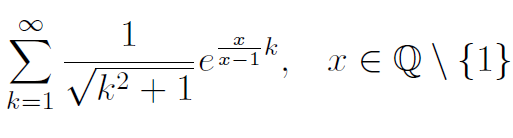
Nun soll ich untersuchen, für welches die die Reihe divergiert bzw. konvergiert. Die Reihe sieht ziemlich unübersichtlich aus. Kann man die eventuell umformen oder mit einer Reihe abschätzen?

LG

Orbi

Comments

Nicht verwirren lassen, schlicht Quotientenkriterium verwenden.

Answer 1

Substituiere \(y:=e^\frac{x}{x-1}\). Dann hast du die Potenzreihe \(\sum\limits_{k=1}^\infty \frac{1}{\sqrt{k^2+1}} y^k\). Davon kannst du den Konvergenzradius bestimmen. Und damit kannst du dann alle \(x\) bestimmen, für die die ursprüngliche Reihe konvergiert.

Comments

Was ist denn ein Konvergenzradius? Ich habe schonmal etwas  davon gehört, in der Vorlesung haben wir so etwas aber nie eingeführt....

---

Warum fragst du nicht Google?

---

Okay, ich habe mich kurz eingelesen.  Es gibt ja einmal den Satz von Cauchy-Hadamard und den von Euler. Selbst wenn ich den Konvergenzradius nun ausrechne, wie sollte dieser mir nun in meiner Rechnung weiterhelfen?

LG

Orbi

---

Könnte da mir einer weiterhelfen? Bin gerade so richtig verwirrt!

---

Hast Du den Konvergenzradius von \(\sum{1\over\sqrt{k^2+1}}y^k\) jetzt ausgerechnet? Ansonsten wuerde ich das mal machen.