Ich mache hier irgendwas falsch,
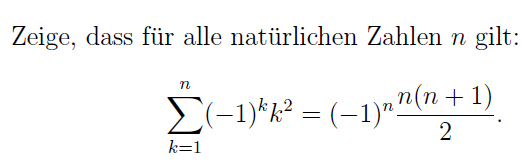
Induktionsanfang: n=1:
(-1)^1*1^2= (-1)^1 ((1(1+1))/2) => -1 = -1 (ok)
Induktionsschritt n-> n+1
∑(k=1,n+1) (-1)^k*k^2 =(-1)^n+1* ((n+1)*(n+2)/2)
∑(k=1,n) (-1)^k*k^2 + (-1)^n * n^2 = (-1)^n * (-1) ((n^2+3n+2)/2)
IV:
(-1)^n (n(n+1)/2)+(-1)^n * n^2= (-1)^n * (-1) ((n^2+3n+2)/2)
kürzen von (-1)^n:
(n^2+n)/2+n^2 = (-1) ((n^2+3n+2)/2)
3n^2+n = -n^2-3n-2
Wo mache ich einen Fehler? :(