Wie zeige ich das f im Punkt (x,y) partiell diff`bar ist? Mein Bsp f(x,y)= max{x,y} in Punkt(1,0)

Question

Wie der Titel schon sagt möchte ich gerne wissen wie man zeigen kann das eine Funktion partiell diff`bar ist.

Zum beispiel behandle ich gerade die Funktion f(x,y)= max{x,y}

Wie kann ich zeigen, dass diese Funktion im Punkte (1,0) diff`bar ist? und vor allem wenn ja wie sehen die Ableitungen in dem punkt aus? Müssten ja alle verschwinden da f(x,y)= 1 ist oder?

Answer 1

Betrachte mal:

https://www.wolframalpha.com/input/?i=f%28x%2Cy%29+%3D+max%7Bx%2Cy%7D

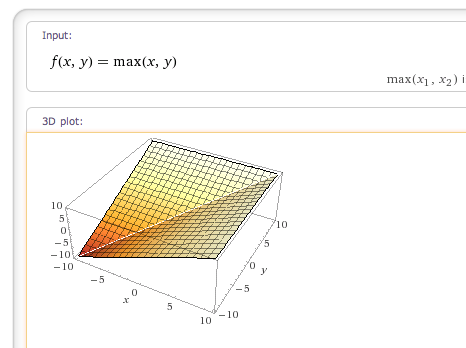
Dort  zeigt dir die 3d-Darstellung, dass die Funktion in y-Richtung die Steigung 0 und in x-Richtung die Steigung 1 hat, in dem Bereich, in dem max(x,y) = x.     (x≥y)

Im andern (x<y) gilt das Gegenteil, da dort max(x,y) = y. Partielle Ableitung nach x ist hier 0 und nach y ist sie 1.

Wo du die partiellen Ableitungen bestimmen kannst, ist die Funktion partiell diff'bar.

Wenn x=y hast du einen Konflikt. Sowohl die Partielle Ableitung nach x als auch jene nach y haben eine Srpungstelle. Deshalb ist f(x,y) nicht partiell diff'bar, falls x=y.

Hier noch die partielle Ableitung nach x gemäss obigem Link zu WolframAlpha. Unstetigkeitsstellen bei x=y gehen aus deren Darstellung nicht explizit hervor. Ist aber ein Sprung von 0 auf 1.