Umkehrfunktion Urbild eines Punktes bestimmen und Umkehrbarkeit folgern

Question

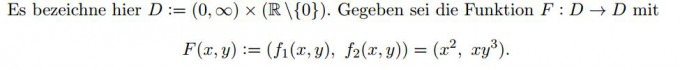
gegeben ist die FUnktion: x^2.xy^3

Zeigen sie lokale Umkehrbarkeit im definitionsbereich, dann das Urbild (x,y) eines beliebigen Punktes (u,v), mit den Def.b. D:=(0,unendlich) X (R\(0))

Folgern sie aus ihren Ergebnissen, eine Aussage über die globale Umkehrbarkeit

Danke für hilfe

-Die lokale Umkehrbarkeit habe ich bereits bestimmt, ida die determinante von den Ableitungen ungleich 0 ist, gibt es eine lokale umkehrbarkeit.

Das Urbild kriege ich allerdings nicht bestimmt, dafür muss man anscheinend eine Umkehrfunktion bilden.

Answer 1

Sei ( u;v) aus D.  Für das Urbild (x;y) muss dann  gelten

u = x^2   und   v = xy^3 

Da x aus ( o; unendlich ) gibt es nur eine Möglichkeit x = wurzel(u) und

das geht immer, weil u>0.

dann ist   v = wurzel(u) * y^3 also , da   wurzel(u)  nicht 0 ist

v / wurzel(u) = y^3 

und wegen v aus IR \ {0} ist   y jetzt auch eindeutig bestimmt

y = sign ( v )  *   3. Wurzel (     abs(  v / wurzel(u) ) ) 

Also gibt es zu jedem Paar (u;v) genau ein Urbild  (x;y) und damit ist

F sogar global umkehrbar.

Comments

danke für die Antowort, dass macht auch Sinn. Ich verstehe nur nicht warum man das macht. Ich verstehe das Prinzip von Umkehren eigentlich, hier erschließen sich mir die schritte nicht,warum man was macht.
Wir haben  u=x^2 und v=xy^3  man würde doch denken, dass man beide nach x und y auflösen sollte oder so und dann die variablen vertauschen? oder machen wir das?

---

Genau das ist doch geschehen.

bei F war es (x;y) → ( x² ; xy³   )  =   ( u;v)

und bei F ^-1 ist es dann

(u;v) ---------------->  ( wurzel(u) ;  sign ( v )  *   3. Wurzel (     abs(  v / wurzel(u) ) ) )

Das kannst du natürlich auch wieder mit (x;y) schreiben

(x;y) ----->  ( wurzel(x) ;   sign ( y )  *   3. Wurzel (     abs(  x / wurzel(y) ) ) ) = F^-1 ( x;y)