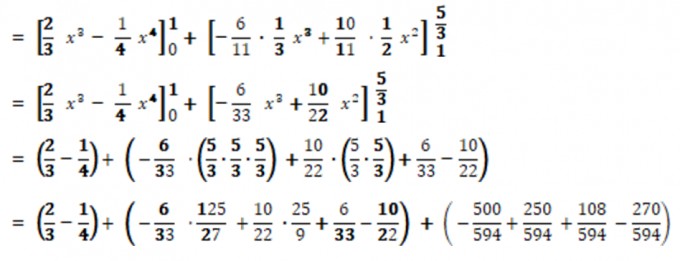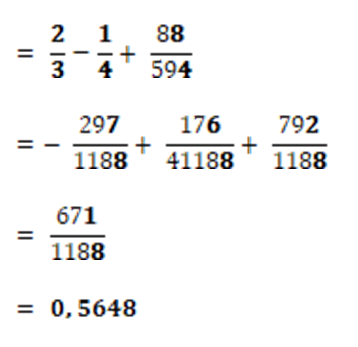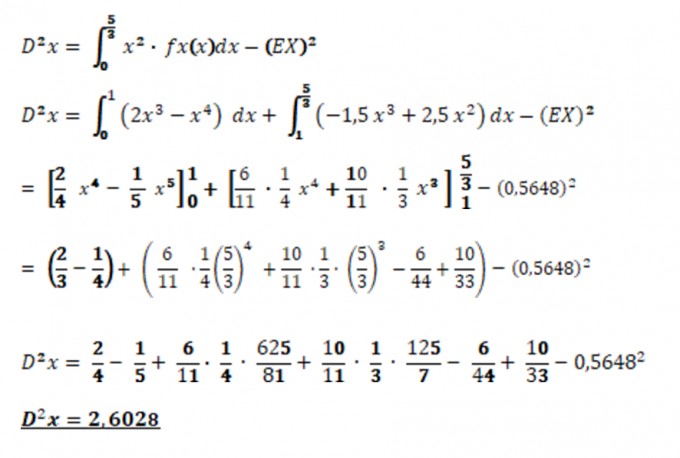Aufgabe 2: Parameterwerte einer Verteilungsfunktion F(x)
Mit reellen Parametern a, b und c ist die folgende Funktion gegeben:
$$ f _ { X } ( x ) = \left\{ \begin{array} { c c } { 2 x - x ^ { 2 } } & { \text { für } 0 \leq x \leq 1 } \\ { a x + b } & { \text { für } 1 < x \leq \frac { 5 } { 3 } } \\ { 0 } & { \text { sonst } } \end{array} \right. $$
Bestimmen Sie die Parameter so, dass f_x stetige Dichtefunktion einer Verteilungsfunktion F_x ist; f_x muss also stetig sein und es muss gelten:
$$ \int _ { \mathbb { R } } f _ { X } ( x ) d x = 1 $$
Aufgabe 3: Erwartungswert und Varianz
Bestimmen Sie Erwartungswert und Varianz der durch die Lösung von Aufgabe 2 definierten Verteilung.
Meine Lösung zur Aufgabe 2:
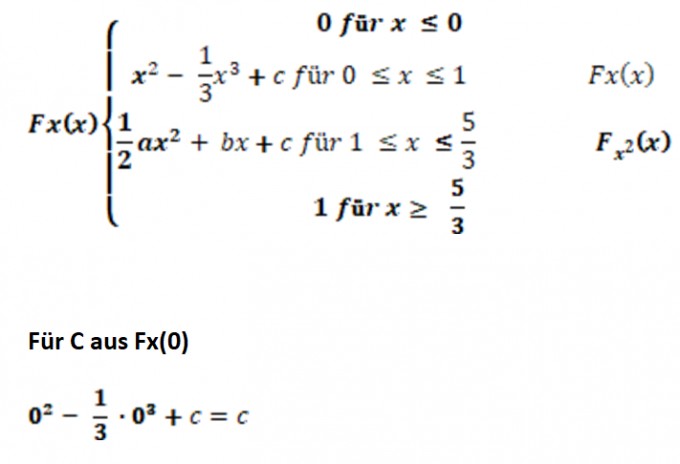
Da mit 0 multipliziert → 0 = c
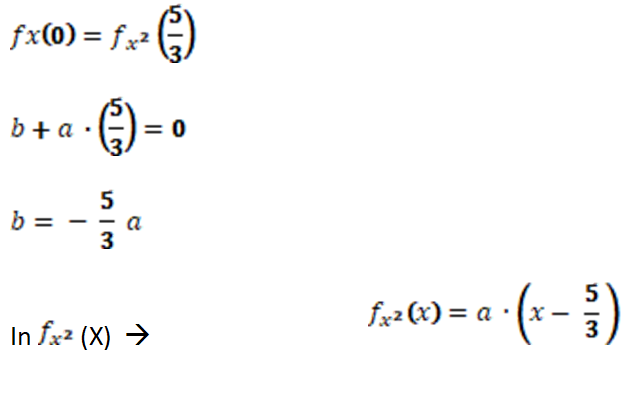
Für fx (X) dx = 1
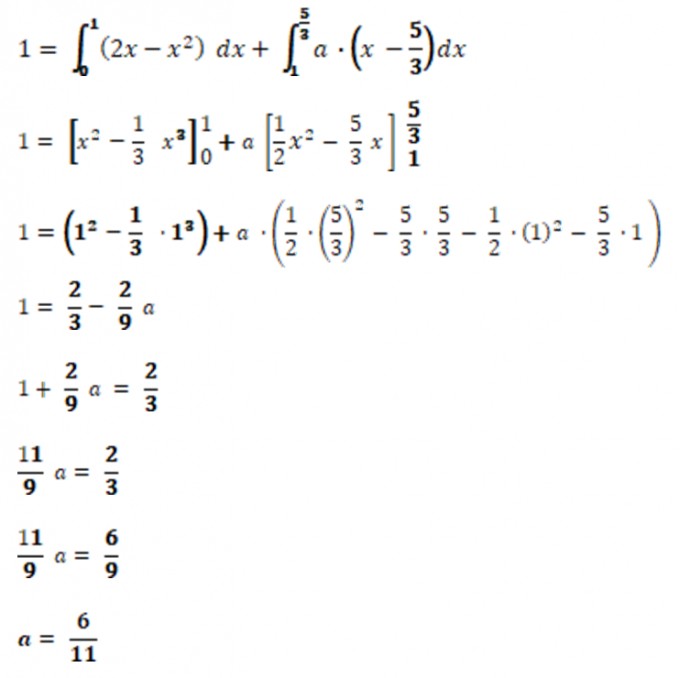
Teil 2:
$$ b = \frac { 5 } { 3 } \cdot \frac { 6 } { 11 } $$
// hier müsste doch – 5/3 hinkommen ?!
$$ b = \frac{10}{11} $$
Meine Lösung zu Aufgabe 3:
$$ E X = \int _ { 0 } ^ { \frac { 5 } { 3 } } x \cdot f x ( x ) d x = \int _ { 0 } ^ { 1 } \left( 2 x ^ { 2 } - x ^ { 3 } \right) d x + \int _ { 1 } ^ { \frac { 5 } { 3 } } \left( - 1,5 x ^ { 2 } + 2,5 x \right) d x $$