Hier liegt vermutlich nur ein primitiver Spezialfall: Geradengleichung (Polynom Grad 1) vor:
§1:
http://www.gerdlamprecht.de/Roemisch_JAVA.htm ergibt
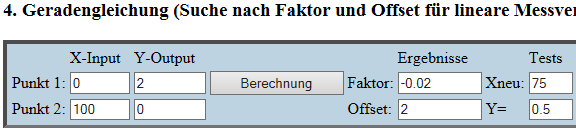
also f(x) = -0.02 + 2 = 2 - x/50
§2: für kompliziertere Stützstellen gibt es Polynominterpolation (etwa bis Grad 10)
http://www.gerdlamprecht.de/Mittelwerte.html
So kann man noch einen Punkt hinzufügen: x=150 und y=9999999 was dann ein Polynom Grad 5 ergibt:
2+x*1999997/150-pow(x,2)*10000/9+pow(x,3)*280/9-pow(x,4)*16/45+pow(x,5)*8/5625
mit pow(x,5)=x^5=x hoch 5 = x*x*x*x*x
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#round((2+x*1999997/150-@Px,2)*10000/9+@Px,3)*280/9-@Px,4)*16/45+@Px,5)*8/5625)*1e4)/1e4@Na=1;b=@Q2);@N@Bi]=i*25;@Ci]=Fx(@Bi]);@Ni%3E8@N0@N0@N#
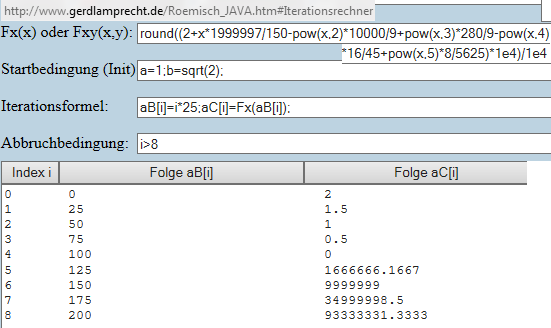
und für andere nichtlineare Funktionswerte gibt es
"Nichtlineare Regression"
http://www.xuru.org/rt/NLR.asp#CopyPaste
Ohne Randbedingungen (also wo die Werte herkommen oder welches Thema Ihr gerade behandelt)
kann man mit Mathematik alles mögliche "basteln", damit die Kurve exakt durch alle 4 Punkte geht.
(ich kenne über 300 Funktionen)
§1 (grün) und §2 (rot) gehen durch selbe Punkte:
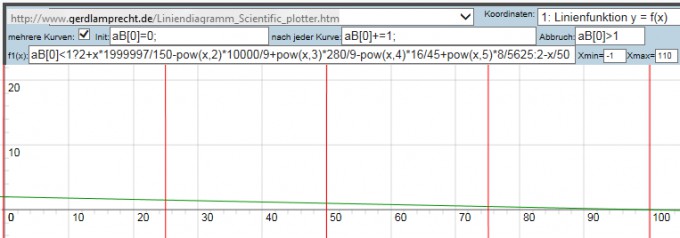
aus Platzgründen wurde rote Kurve oben & unten abgeschnitten.