Kreisgleichung bestimmen von Kreis mit Mittelpunkt und Geraden

Question

Hallo =)

Ich brauche st Hilfe und zwar weiss ich nicht wie nicht wie ich bei dieser Aufgabe vorgehen soll =S

Aufgabe:

Ein Kreis mit dem Mittelpunkt auf der Geraden a: x-2y-1=0 berührt die Geraden b: 3x+4y+22=0 und c: 4x-3y+46= 0

Bestimme die Kreisgleichung

 

Vielen Dank für jede Hilfe!!!

Answer 1

Du würdest von b und c die Winkelhalbierende bestimmen und dann den Schnittpunkt der Winkelhalbierenden mit a bilden. Das wäre dann der Mittelpunkt des Kreises. Dann bestimmst Du den Abstand vom Mittelpunkt zu einer Tangente und erhältst den Kreisradius. Damit kannst du dann deine Kreisgleichung aufstellen.

Comments

Ich habe die Winkelhalbierende berechnet von b und c und bekomme:

x-7y+24=0           und           7x+y+68=0

doch wie kann ich jetzt den Schnittpunkt mit a bilden?

---

Deine Winkelhalbierenden sind beide richtig.

x - 7y + 24 = 0
x - 2y - 1 = 0

Das ist ein LGS was man mit dem Additionsverfahren lösen kann

I - II

25 - 5·y = 0
y = 5

x - 2*5 - 1 = 0
x = 11

Schnittpunkt hier ist also M1(11 | 5)

So machst du das jetzt auch noch mit der 2. Winkelhalbierenden. Danach dann nur noch den Radius ausrechnen indem du den Abstand von M zu einer Geraden bestimmst.

 

---

Vielen   Hab es endlich begriffen =)

Answer 2

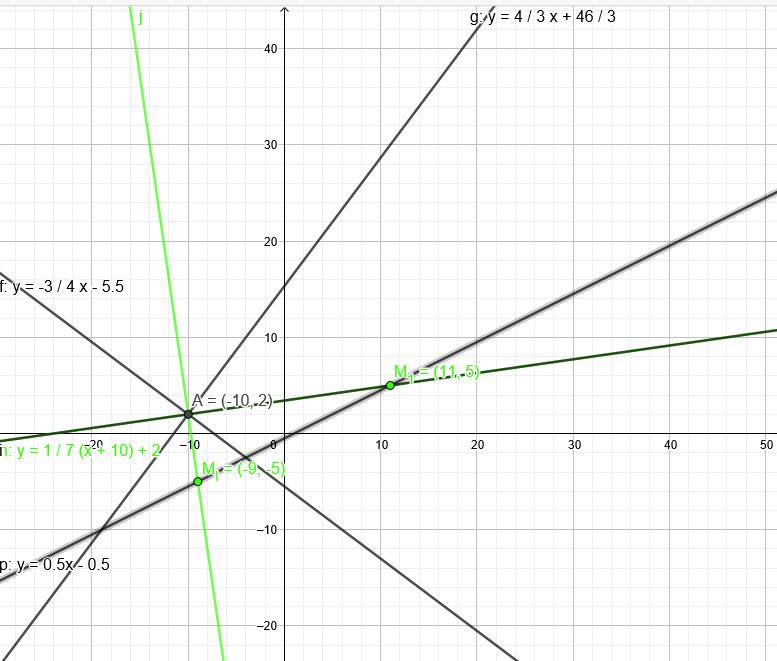
Mittelpunktsgerade: \(x-2y-1=0\)     \(y=0,5x-0,5\)
1.Tangente:
\( 3x+4y+22=0 \)  →  \( y=-\frac{3}{4}x-5,5 \)
2.Tangente:
\( 4x-3y=-46 \)  →  \( y=\red{\frac{4}{3}}x+\frac{46}{3} \)
Berechnung der Winkelhalbierenden:

Die beiden Tangenten stehen senkrecht auf einander → \(45°\)   zwischen der Winkelhalbierenden und den beiden Tangenten.

\(tan(α)= \frac{m_2-m_1}{1+m_1*m_2} \)

\(tan(45)= \frac{\red{\frac{4}{3}}-m_1}{1+m_1*\red{\frac{4}{3}}} =1\)

\( \frac{4}{3}-m_1=1+m_1*\frac{4}{3} \)

\( m_1+m_1*\frac{4}{3}=-1+\frac{4}{3}=\frac{1}{3} \)

\( \frac{7}{3}m_1=\frac{1}{3} \)

\( m_1=\frac{1}{7} \)

\(\frac{y-2}{x+10}=\frac{1}{7} \)

\(y=\frac{1}{7}*(x+10)+2 \)

Es gibt noch eine 2. Winkelhalbierende.