Gib eine Gleichung des Kreises k1 an, der durch die Punkte A und B geht und dessen Mittelpunkt auf k2 liegt

Question

A=(-2/3)

B=(2/-1)

k2=(x-5)²+(y-4)²=4

Comments

Testgrafik
~plot~ sqrt(4-(x-5)^{2} ) + 4 ; 4 - sqrt(4-(x-5)^{2} )  ;{-2|3};{2|-1}  ; [[ -3 | 10 | -2 | 10 ]] ~plot~

---

bessere Graphik
Kreis k_1.ggb (10 kb)

---

ich bräuchte den rechenweg
LG

---

Ein beliebiger Kreis erfüllt die Gleichung

(x-a)^2+(y-b)^2=r^2

Mit Mittelpunkt (a,b) und Radius r.

Mit den obigen Bedingungen erhältst du 3 Gleichungen mit 3 Unbekannten, die du lösen kannst.

---

Heute abend ist es mir zur Beantwortung  zu spät.

Es muß nachgeschaut werden ob ein Punkt auf dem Kreis
denselben Abstand zu A und B hat.

mfg Georg

---

~plot~ sqrt(4-(x-5)^{2})+4;4-sqrt(4-(x-5)^{2}) ;6-sqrt(58-(x-5)^{2});{-2|3};{2|-1} ;[[-3|10|-2|10]] ~plot~

M ( 5 | 6 ) r^2 = 58

Die Berechnung

y = 6
x = 5

---

Hallo Georg,

es gibt zwei Kreise mit den gegebenen Bedingungen (vgl. meine Antwort)

Gruß Wolfgang

---

Hallo Wolfgang,

ich habe hier nur eine Lösung angeführt weil du die 2. Lösung
bereits angeführt hattest.
Meine Lösung ist vom Ansatz her vielleicht einfacher aber es
würde mehr ( manuell ) zu rechnen geben.
Ich will es daher dem Fragesteller überlassen ob er Nachfragen hat.

mfg Georg

Answer 1

der Mittelpunkt des gesuchten Kreises muss von A und B die gleiche Entfernung haben. Er muss also auf der Mittelsenkrechten der Strecke AB liegen.

Der Mittelpunkt von \(\overline{AB}\) ist  ( (-2+2) / 2 | (3 + (-1)) / 2 ) = (0|1)

Die Steigung von Gerade AB ist  (3 - (-1)) / (-2 - 2) = 4 / (-4) = -1

→ Die Mittelsenkrechte enthält den Punkt P(0|1) und hat die Steigung 1

→  Gleichung der Mittelsenkrechten:  y = x  + 1

Einsetzen in die Kreisgleichung (x-5)²+(y-4)²=4 :

(x-5)² + (x+1 - 4)² = 4

 x²  - 8·x + 15 = 0

x² + px + q = 0

pq-Formel:  p = - 8 ; q = 15

x_1,2 = - p/2 ± \(\sqrt{(p/2)^2 - q}\)

x_1,2 = 4 ± \(\sqrt{16 - 15}\)

x₁ = 5  , x₂ = 3    →  y₁ = 6 , y₂ = 4  

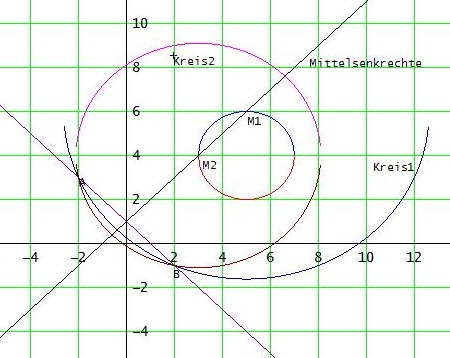
→  M₁(5|6)  oder  M₂(3|4)  für die gesuchte Kreisgleichung.

r₁ = | \(\overline{AM_1}\) |   = √ [ (-2 - 5)² + (3 - 6)² ]  = √58

r₂ = | \(\overline{AM_2}\) |   = √ [ (-2 - 3)² + (3 - 4)² ]  = √26

Es gibt also zwei Möglichkeiten für die gesuchte Kreisgleichung:

(x - 5)² + (y - 6)²  = 58       oder      (x - 3)² + (y - 4)² = 26

Gruß Wolfgang