Ermittle eine Gleichung des Kreises durch A und B, dessen Mittelpunkt auf g liegt! A=(7/5) , B=(5/5) , g:5x-y=4

Question

Ermittle eine Gleichung des Kreises, der durch die Punkte A und B geht und dessen Mittelpunkt auf der Geraden g liegt!

A=(7/5) , B=(5/5) , g:5x-y=4

Hinweis: Streckensymmetrale!

Answer 1

Die allgemeine Formel für einen Kreis lautet

(x-a)^2 + (y-b)^2 = r^2

Setzt man die beiden Gegebenen Punkte ein, erhält man gemeinsam mit der dritten Gleichung das nichtlineare Gleichungssystem:

(7-a)^2 + (5-b)^2 = r^2
(5-a)^2 + (5-b)^2 = r^2
5a - b = 4

Man kann zunächst die dritte Gleichung nutzen, um b durch a auszudrücken:

b = 5a - 4

Eingesetzt in die ersten beiden Gleichungen erhält man damit:

(7-a)^2 + (9 - 5a)^2 = r^2
(5-a)^2 + (9 - 5a)^2 = r^2

Subtrahiert man die zweite Gleichung von der ersten, erhält man:

(7-a)^2 - (5-a)^2 = 0

49 - 14a + a^2 - 25 + 10a - a^2 = 0

24 - 4a = 0

a = 6

Damit kann man nun zunächst b bestimmen:

b = 5*6 - 4 = 30 - 4 = 26

Und für den Radius erhält man z.B. aus der ersten Gleichung:

(7-6)^2 + (9-5*6)^2 = r^2

1^2 + 21^2 = r^2

r^2 = 442

r ≈ 21.024

 

Die Gleichung des Kreises lautet also:

(x-6)^2 + (y - 26)^2 = 442

Answer 2

Wir brauchen die Mittelsenkrechte von AB

Die Steigung zwischen A und B ist 0

Damit lautet die Mittelsenkrechte 

x = 6

5x - y = 4
5*6 - y = 4
y = 26

Der Mittelpunkt liegt bei M = [6, 26]

Nun brauchen wir noch den Abstand von A zu M

|AM| = √((7 - 6)^2 + (5 - 26)^2) = √442

Damit lautet die Kreisgleichung

(x - 6)^2 + (y - 26)^2 = 442

Hier eine Skizze:

Comments

hallo Mathecoach,

kannst du mir erklären wie du auf x=6 gekommen bist ?

Wenn ich AB habe

---

A=(7/5) , B=(5/5)

Bei x = 6 liegt der Mittelpunkt zwischen A und B

---

Und \((6|5)\) ist der Mittelpunkt der Strecke \(AB\).

---

Die Frage ist aus dem Jahr 2013?

Grummel...

---

Ich bin eigentlich froh, dass es Leute gibt, die noch unter den alten Fragen nachsehen und nicht ihr Anliegen gleich ohne zu suchen als neue Frage stellen.

---

Hat der FS aber nicht getan. Die Antworten wurden wohl zusammengeführt.

---

Ok, das ist mir zu unübersichtlich!             

Answer 3

wie soll ich aus der Geraden den Mittelpunkt herausfinden ?

Du stellst für die Punkte A und B die Geradengleichung
auf und errechnest dann den Schnittpunkt mit der
bereits gegebenen Gleichung.

Comments

Ich denke nicht, dass die Gerade AB die gegebene Gerade im Mittelpunkt des gesuchten Kreises schneidet.

vgl. meine Antwort

---

Hier eine Korrektur

A (7/5)
B (5/5)

Die beiden Punkte liegen auf der Geraden
y = 5
Der Mittelpunkt ist bei x = 6
Die Normale ist somit x = 6
( eine Senkrechte )

Schnittpunkt mit der Geraden
5x - y = 4
y = 5 * x + 4

x = 6
y = 5 * 6 + 4 = 34

M ( 6 | 34 )

Der Abstand vom M zu A ( oder B ) ist r

r^2 = ( 34 - 5 ) ^2  + ( 6 - 7  ) ^2
r = 29.02

r^2 = ( x - 6 ) ^2 + ( y - 34 ) ^2
29.02^2 = ( x - 6 ) ^2 + ( y - 34 ) ^2

---

5x - y = 4 
y = 5 * x + 4

x = 6 
y = 5 * 6 + 4 = 34 

Hier muss es y = 5*6 - 4 = 26 heißen

---

Nochmalige Korrektur

x = 6
y = 5 * 6 - 4 = 26

M ( 6 | 26 )

Der Abstand vom M zu A ( oder B ) ist r

r² = ( 26 - 5 ) ²  + ( 6 - 7  ) ²
r^2 = 442
r = 21.02

r² = ( x - 6 ) ² + ( y - 26 ) ²
442 = ( x - 6 ) ² + ( y - 26 ) ²

Answer 4

Hallo bg,  

allgemeine Antwort wegen Sonderfall  m_AB = 0 geändert:

die Strecke AB  hat den Mittelpunkt   P ( (x_A+x_B) /2 | (y_A + y_B) / 2 )  = P(6|5)

Die Gerade AB  hat die Steigung m_AB = (y_A - y_B) / (x_A - x_B) = 0

Die Mittelsenkrechte von AB hat dann die Gleichung  x = 6

Die Mittelsenkrechte musst du mit der gegebenen Geraden schneiden

5 * 6 - y = 4 →  y = 26    →  M(6|26)  für den Mittelpunkt des Kreises

Dessen Entfernung von A ist der Radius r des Kreises:

          r = √[ (x_A - x_M)² + (y_A - y_M)² ]  = √(1² +(- 21) ²) = √442

Kreisgleichung:  (x - x_M)² + (y - y_M)² = r²  , also :  (x - 6)² + (y - 26)² = 442  

Gruß Wolfgang

Comments

Hallo Wolfgang,
die Berechnungen reduzieren sich drastisch
weil (y_A = y_B) ist..
siehe meine Korrektur.

---

Habe die allgemeine Antwort inzwischen geändert, weil hier der Sonderfall vorliegt, dass die Grade AB die Steigung 0 hat.

---

Unten muß es

- 26)² = 442  heißen

---

Danke, habe den Tippfehler korrigiert.

Das war bei uns beiden alles viel Lärm um nichts, weil schon vor 4 Jahren die gleiche Frage beantwortet wurde.

---

ich bedanke mich bei euch ! ich habe die Frage nochmal gestellt weil ich die Antwort auf die andere Frage nicht ganz verstanden habe

---

Dann hat das Forum seinen Zweck erfüllt.
Frag´ solange nach bis du es verstanden hast.
Falls du weitere Fragen hast dann wieder einstellen.

---

habe vor kurzem eine Frage gestellt

---

Es sollte wohl besser  "Frage solange nach ... " heißen  :-)

Ein Link zur alten Frage hätte die Sache vereinfacht.

Answer 5

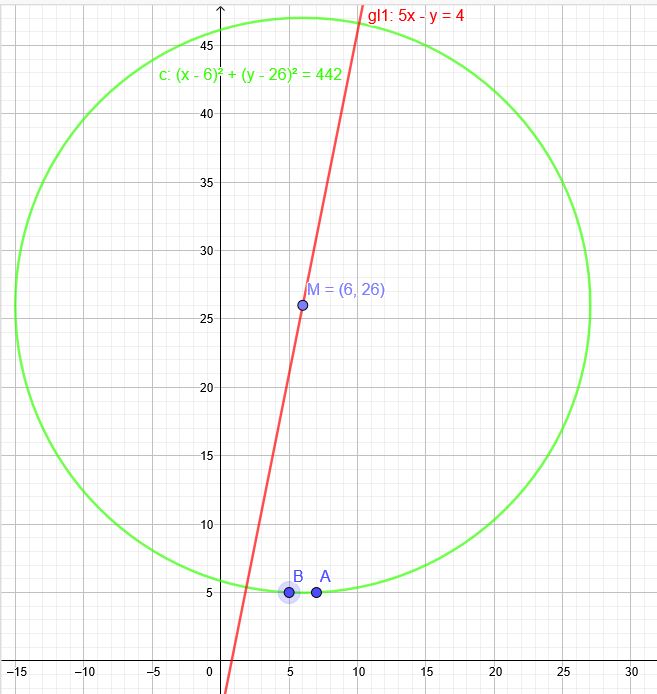
Ermittle eine Gleichung des Kreises, der durch die Punkte A und B geht und dessen Mittelpunkt auf der Geraden g liegt!   \(A(7|5)\) , \(B(5|5)\) , g:  \( 5x-y=4\)

\((x-x_M)^2+(y-y_M)^2=r^2\)

\(A(7|5)\)

1.)  \((7-x_M)^2+(5-y_M)^2=r^2\)

\(B(5|5)\)

2.)  \((5-x_M)^2+(5-y_M)^2=r^2\)

3.)  \( 5x_M-y_M=4\) →   \( y_M=5x_M-4\)  ∈ 1.)  \((7-x_M)^2+(5-5x_M-4)^2=r^2\)

\( y_M=5x_M-4\)  ∈ 2.)  \((5-x_M)^2+(5-5x_M-4)^2=r^2\)

1.)  \((7-x_M)^2+(1-5x_M)^2=r^2\)

2.)  \((5-x_M)^2+(1-5x_M)^2=r^2\)

1.) -2.):

\((7-x_M)^2-(5-x_M)^2=0\)

3.Binom

\([(7-x_M)-(5-x_M)][(7-x_M)+(5-x_M)]=0\)

1.)

[7-x_M-5+x_M)]=0 geht nicht

2.)

[(7-x_M+5-x_M)]=0

\(x_M=6\)  \( y_M=5\cdot 6-4=26\)

\((7-6)^2+(5-26)^2=r^2\)

\(r^2=442\)

\((x-6)^2+(y-26)^2=442\)