Funktionentheorie Kurvenlängen und -integrale

Question

Hallo miteinander!!!

Ich lerne gerade für die Funktionentheorieklausur und komme mit einigen Aufgaben nicht zurecht. Wenn jemand mir helfen würde, wäre ich sehr dankbar. :)

Die Aufgabe:

Betrachten Sie die Kurve Γ=[γ], die durch γ: [0, π/2] → ℂ, γ(t):= sin(t)+i*(1-cos(t)), 0 ≤ t ≤ π/2 parametrisiert wird.

a) Bestimmen Sie die Länge len Γ von Γ (dafür habe ich zu viele Formeln gefunden, weiss nicht welche richtig ist)

b) Bestimmen Sie die Kurvenintegrale 

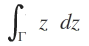  und  

Answer 1

$$ Ableitung y ' (t) = cos(t)+i*sin(t) $$
$$ l = \int_{0}^{\frac { pi }{ 2 }}|(cos(t)+i*sin(t))|dt $$
$$ = \int_{0}^{\frac { pi }{ 2 }} 1 dt $$
$$ =[ t ] in den Grenzen von 0 bis pi/2  = pi/2 $$

Kein Wunder, die Kurve ist ein verschobenes Viertel vom Einheitskreis.

Comments

Vielen Dank für die Hilfe ☺ Ich habe versucht mit der eulerschen formel zu lösen, aber habe was anderes bekommen . Habe ich irgendwo einen Fehler gemacht? 

---

Ich habe meinen Fehler gefunden, abs(e^it) ist 1, wenn t positiv ist. !!

Answer 2

Fuer die Kurvenlaenge gibt es nur eine Formel: \(\ell=\int_a^b|\gamma'(t)|\,dt\). Die Ableitung geht besser, wenn man \(\gamma\) mit der Eulerschen Formel umschreibt.