Deine Konstruktion war doch völlig ok bis auf die Lücke "Rechter Winkel", auf die ich hingewiesen hatte.
Ein rechter Winkel ist nun allerdings folgendermaßen zu konstruieren :
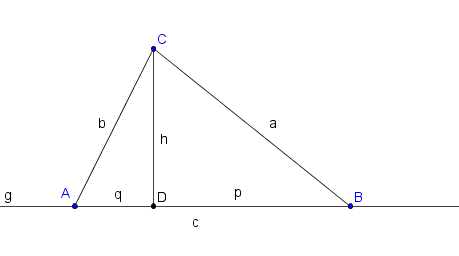
Zeichne wie dargestellt ein ΔABC.
Der Winkel bei D wird ein rechter sein, wenn a² = h² + p² und b² = h² + q² ist.
Subrtraktion der Gleichungen liefert a² - b² = p² - q² = (p+q)·(p-q)
und somit p - q = (a² - b²) / c .
Messung von a, b und c (und ein wenig Rechnung) ergeben also die
Streckenlängen p+q und p-q und damit auch p und q selbst also letztlich die Lage des Punktes D.
Dies setzt allerdings voraus, dass mit dem "Zentimeterlineal" beliebige, auch irrationale Streckenlängen gemessen und abgetragen werden können.
Meine eigene Lösung (die wahrscheinlich auch die von MC ist) verschiebt die eine Gerade parallel, so dass ein Schnittpunkt mit der anderen auf dem Zeichenblatt entsteht, konstruiert dann die Winkelhalbierende nach der von MC dargestellten Methodeund schiebt die Gerade anschließend unter Mitnahme der Winkelhalbierenden (in Richtung der anderen Geraden) zurück.