Beweise: Es existiert beschränkte nichtkonstante holomorphe Funktionen auf F, wenn F⊂ℂ ein beschränktes Gebiet.

Question

Hallo Liebe Leute,

ich lerne gerade auf meine Klausur in Ana4 und komm mit dem Beweis gar nicht klar und weiter...

Vielleicht kann mir da jemand weiterhelfen, worüber ich mich echt riesig freuen würde.

Meine Frage :

1.Sei F⊂ℂ ein beschränktes Gebiet. Dann existiert beschränkte nichtkonstante holomorphe Funktionen auf F.

Ich hoffe es kann mir jemand helfen.

Vielen Dank schonmal an alle :)

Lieben Gruß
Chrsitina

Comments

"1.Sei F⊂ℂ ein beschränktes Gebiet. Dann existiert beschränkte nichtkonstante holomorphe Funktionen auf F."

Wenn das wirklich die Frage ist, lautet die Antwort: Klar, z.B.: \(id|_F\).

---

Das war wirklich die Frage
man sollte es mit den Sätzen beweisen :)
dankeauch für deine Antwort :)
Lieben Gruß

---

Zu beweisen gibt es nur dann was, wenn die Frage anders lautet, z.B. dass F das Holomorphiegebiet der Funktion sein soll.

---

hmmm

meinst du so gibt es nichts zu beweisen?

die frage lautet nämlich genauso wie ich sie gestellt habe.

Answer 1

Grundsätzlich gilt

 

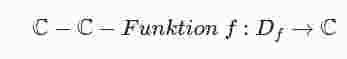
heißt holomorph im Gebiet G ⊆ G_f (an der Stelle a ∈ D_f), wenn f an jeder Stelle von G (in einer offenen Umgebung von a) komplex differenzierbar ist. 

Ist f an der Stelle a holomorph, so existiert 

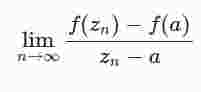
für jede Folge (z_n) mit 

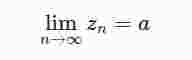
Existieren nun die partiellen Ableitungen von u und v und wählt man speziell z_n=a + h_1n mit h_1n∈ℝ und 

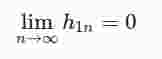
, so gilt:

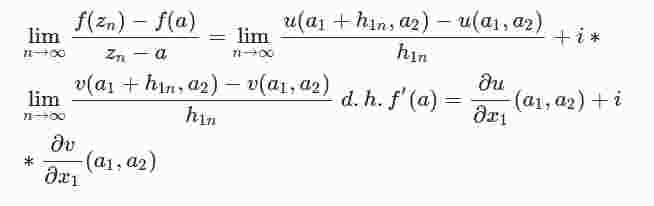
Setzt man anderseits z_n = a + ih_2n mit h_2n∈ ℝ und

 

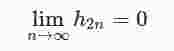
, so erhält man 

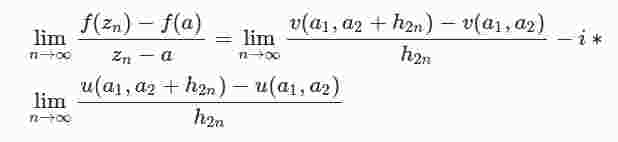
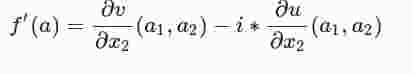
Ein Vergleich liefert das Erfülltsein der sog. Cauchy-Riemannschen Differentialgleichungen 

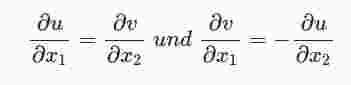
an der Stelle (a₁,a₂).

Mit Hilfe des Mittelwertsatzes kann aus dem Erfülltsein der Gleichung in einer offenen Umgebung eines Punktes auch umgekehrt auf Holomorphie an dieser Stelle geschlossen werden. Es gilt somit 

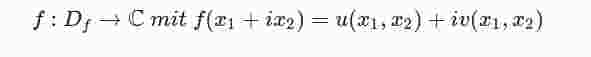
ist in a ∈ D_f mit a = a₁ + ia₂ genau dann holomorph, wenn u und v in einer Umgebung von (a₁,a₂) stetig partiell differenzierbar sind und dort die Cauchy-Riemannschen Differentialgleichungen erfüllt sind.

Während in ℂ jedes Gebiet G Holomorphiegebiet ist in dem Sinne, dass es eine in G holomorphe Funktion gibt, die nicht über G hinaus analytisch fortsetzbar ist, gibt es in ℂⁿ, n ≥ 2 Gebiete, aus denen jede dort holomorphe Funktion in ein echt umfassendes Gebiet analytisch fortgesetzt werden kann. 

Ist 

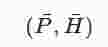
eine allgemeine Hartogsfigur und f in H holomorph, so auch in der umfassenden Menge P. 

Jetzt kommen wir zum eigentlichen Beweis:

Wie bei reellen Funktionen mit mehreren Variablen kommt man auch bei komplexen Funktionen über die lineare Approximierbarkeit an einer Stelle a zum Begriff der komplexen Differenzierbarkeit an dieser Stelle. Er ist für eine Funktion 

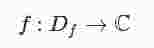
im Gebiet

 

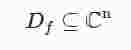
gleichbedeutend mit der Existenz stetiger partieller Ableitungen

 

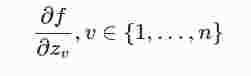
, an der Stelle a. Eine Funktion heißt holomorph in einem Gebiet, wenn sie an jeder Stelle des Gebietes komplex differenzierbar ist.

Führt man mittels f = u + iv die Funktion f auf zwei reellwertige Funktionen mit 2n Variablen 

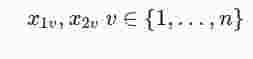
zurück, so reicht für komplexe Differenzierbarkeit noch nicht die stetige partielle Differenzierbarkeit von u und v nach diesen 2n Variablen aus. Eine Übertragung der Rechnung, die zur Aufstellung der Cauchy-Riemannschen Differentialgleichungen führt, liefert

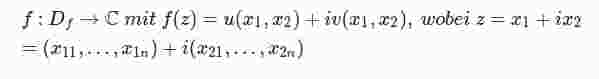
gilt ist genau dann einer Umgebung der Stelle a = a₁ + ia₂ holomorph, wenn die ℝ²ⁿ-ℝ-Funktionen u und v in einer Umgebung von (a₁,a₂) stetig partiell differenzierbar sind und dort die Gleichungen

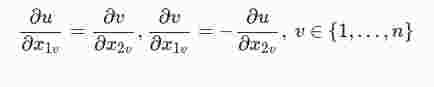
erfüllt sind.

Comments

Hi

ich bedanke mich sehr für diese tolle und ausführliche antwort :)

vielen lieben dank ich werde mir jetzt alles gründlich einarbeiten :)

Lieben Gruß