Wie breit ist der Fluss?

Question

Von einem 50m hohen Turm sieht man in senkrechter Richtung das diesseitige Ufer eines Flusses unter dem Tiefenwinkel α= 58,6° und das jenseitige Ufer unter dem Tiefenwinkel β= 28,9°. Wie breit ist der Fluss?

Comments

Hmm entweder verstehe ich den Text nicht richtig oder die Aufgabenstellung ist schräg. Müsste der Winkel zum jenseitigen Ufer nicht der größere sein?

---

Hallo Kofi123,

nein. Den Standpunkt in die Mitte eines Koordinatensystem
gelegt bedeutet dann
zum dieseitigen Ufer : minus 58.6 ° ( Tiefenwinkel 58.6 ° )
zum gegenüberliegenden Ufer :  minus 28.9 ° ( Tiefenwinkel 28.9 ° )

Die Aufgabe ist richtig gestellt.

---

Ah, ich hab mal den Tiefenwinkel gegoogelt. Der Winkel wird quasi auf Höhe der Turmspitze gegenüber einer gedachten Horizontalen nach unten gemessen. Dann macht es Sinn.

Answer 1

50/TAN(28.9°) - 50/TAN(58.6°) = 60.05 m

Hier eine Skizze wie es zu verstehen ist

Answer 2

Hier die Skizze

zum diesseitigen Ufer

tan ( 58.6 ) = 50 / a
a = 30.52 m

zum gegenüberliegenden Ufer

tan ( 28.9 ) = 50 / b
b = 90.57 m

b - a = 60.05 m

Answer 3

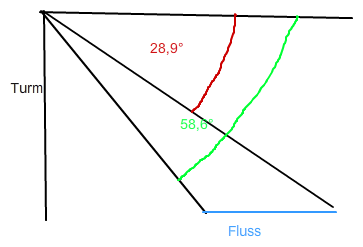
Tiefenwinkel und Steigungswinkel werden immer gegen die Horizontale gemessen.

Du kannst dir so natürlich die Winkel zwischen Turm und den "Blickstrahlen"

ausrechnen und dann mit dem tan die Entfernung vom Turm zum

Fluss und im anderen Fall diese Entfernung+Breite des Flusses

ausrechnen.