Volumsberechnung einer um die y-Achse rotierenden Fläche

Question

Die Fläche zwischen der Kurve (f(x) = x⁴ - 8x² + 16) und der x Achse beträgt 34,13333 FE.

Diese rotiert um die y-Achse. Wie groß ist das Volumen?

Comments

Wenn du dir das Video hier anguckst, sollte die Aufgabe klar sein, geht ganz analog: https://www.youtube.com/watch?v=5ewTO8DUazM

---

xD genau das Video hab ich mir vor geschätzten 10 min angesehen

---

Passiert nun mal wenn man stumpf "rotationsvolumen y achse" bei google eingibt. :P Wenn du dein Ergebnis überprüfen lassen möchtest, kannst du das gern hier reinschreiben.

---

Welches Ergebnis? xD Ich scheiter schon an der Umkehrfunktion. (beim nach x auflösen)

Answer 1

Die Funktion hat die Nullstellen x = ± 2:

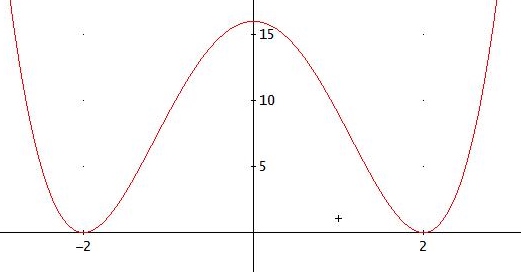
Wegen der Symmetrie genügt es, das Flächenstück zwischen den Achsen und dem Graph über [ 0; 2 ] um die y-Achse rotieren zulassen. Über [0;2] ist der Graph injektiv.

Das Rotationsvolumen beträgt  V = π • ∫₀¹⁶   x² dy   [y-Grenzen!]  f(0) = 16]

Erfreulicherweise lässt sich x² mit wenig Aufwand durch y ausdrücken:

x⁴ -8x +16 = y  <=>  (x² - 4)² = y  <=>  x² - 4 = ± √y  => x² = 4 -√y , da x² -4 in [0;2] negativ ist.

Also: V = π • ∫₀¹⁶ (4 - √y) dy  =  [ 4y - 2/3 • y^3/2 ]₀¹⁶ = 64/3 ≈ 21,33

Comments

Habe leider nach dem integrieren das π vergessen:

Antwort = 21,33 π