Aufgabe:
Berechne das Volumen, welches entsteht, wenn die eingeschlossene Fläche um die x-Achse rotiert.
Gegebene Funktionen: Hyperbel x^2-(y^2/4)=1 und Parabel y^2=6x
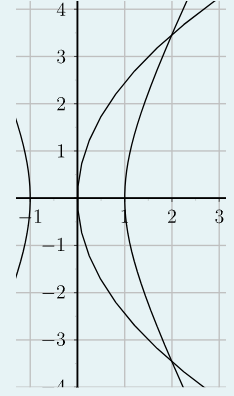
Problem/Ansatz:
Wir haben die Formel für die Berechnung das Volumen von Rotationskörpern gelernt. Diese funktioniert hier jedoch nicht.
Ich denke, man muss auf jeden Fall die Gleichungen auf y bzw y^2 umstellen.
Jedoch weiß ich ab da auch nicht mehr weiter, weil eben der normale Weg nicht funktioniert.