Aufgabe:
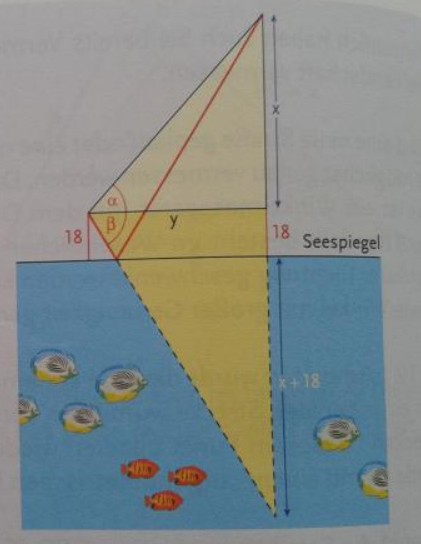
Ein Beobachter, der sich auf einem Turm \( 18 \mathrm{~m} \) über der Fläche eines Sees befindet, beobachtet einen Ballon unter einem Höhenwinkel von \( \alpha=54,537^{\circ} \) und dessen Spiegelbild im Wasser unter einem Tiefenwinkel von \( \beta=57,68^{\circ} \).
Wir ermitteln, wie hoch sich der Ballon über dem See befindet.
Wir arbeiten mit den beiden eingezeichneten rechtwinkeligen Dreiecken:
1. \( \tan \alpha=\frac{x}{y} \)
\( \begin{aligned} \text { 2. } \tan \beta &=\frac{x+36}{y}, \text { also } \\ \frac{\tan \alpha}{\tan \beta} &=\frac{x}{x+36} \\ x &=\frac{36 \cdot \tan \alpha}{\tan \beta-\tan \alpha} \approx 285,92 \end{aligned} \)
Der Ballon befindet sich etwa \( 286 \mathrm{~m}+18 \mathrm{~m} \), also etwa \( 304 \mathrm{~m} \) über dem Seespiegel.
Ansatz/Problem:
Grundsätzlich verstehe ich das Beispiel, welches sich als Bild bei meiner Frage befindet.
Was ich allerdings nicht weiß ist wie man nach Schritt 1 und 2 die Formel so umformt das man x erhält.
Es wäre nett wenn mir jemand die Umformschritte erklären bzw. einfach nur aufschreiben kann.